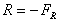We have all seen moving fluids exerting forces. The lift force on an aircraft is exerted by the air moving over the wing. A jet of water from a hose exerts a force on whatever it hits. In fluid mechanics the analysis of motion is performed in the same way as in solid mechanics - by use of Newton's laws of motion. Account is also taken for the special properties of fluids when in motion.

The momentum equation is a statement of Newton's Second Law and relates the sum of the forces acting on an element of fluid to its acceleration or rate of change of momentum. You will probably recognise the equation F = ma which is used in the analysis of solid mechanics to relate applied force to acceleration. In fluid mechanics it is not clear what mass of moving fluid we should use so we use a different form of the equation.

Newton's 2^nd Law can be written:

The Rate of change of momentum of a body is equal to the resultant force acting on the body, and takes place in the direction of the force.

To determine the rate of change of momentum for a fluid we will consider a streamtube as we did for the Bernoulli equation,

We start by assuming that we have steady flow which is non-uniform flowing in a stream tube.

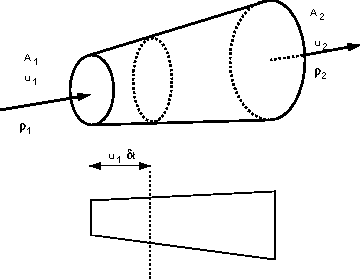
A streamtube in three and two-dimensions

In time 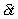a volume of the fluid moves from the inlet a distance 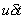, so the volume entering the streamtube in the time 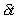is

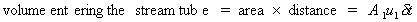
this has mass,

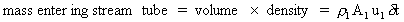
and momentum

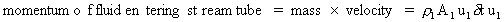
Similarly, at the exit, we can obtain an expression for the momentum leaving the steamtube:

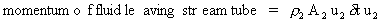
We can now calculate the force exerted by the fluid using Newton's 2^nd Law. The force is equal to the rate of change of momentum. So

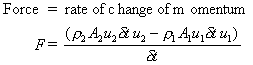
We know from continuity that 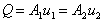, and if we have a fluid of constant density, i.e. 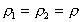, then we can write

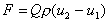
For an alternative derivation of the same expression, as we know from conservation of mass in a stream tube that

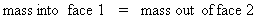
we can write

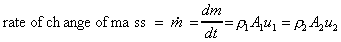
The rate at which momentum leaves face 1 is

The rate at which momentum enters face 2 is

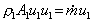
Thus the rate at which momentum changes across the stream tube is

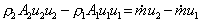
i.e.

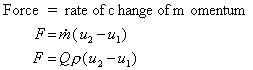
This force is acting in the direction of the flow of the fluid.

This analysis assumed that the inlet and outlet velocities were in the same direction - i.e. a one dimensional system. What happens when this is not the case?

Consider the two dimensional system in the figure below:

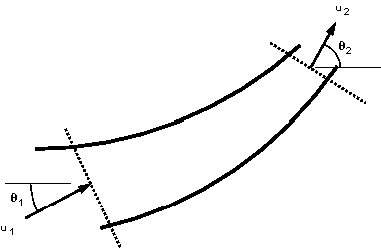
Two dimensional flow in a streamtube

At the inlet the velocity vector, 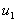, makes an angle, 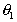, with the x-axis, while at the outlet 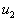make an angle 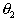. In this case we consider the forces by resolving in the directions of the co-ordinate axes.

The force in the x-direction

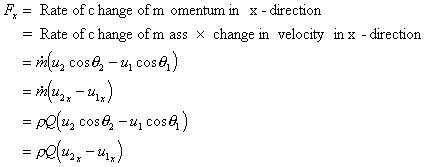
And the force in the y-direction

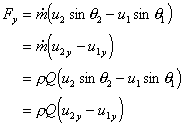
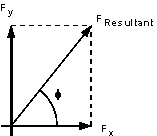
We then find the resultant force by combining these vectorially:

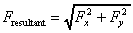
And the angle which this force acts at is given by

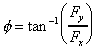
For a three-dimensional (x, y, z) system we then have an extra force to calculate and resolve in the z-direction. This is considered in exactly the same way.

In summary we can say:

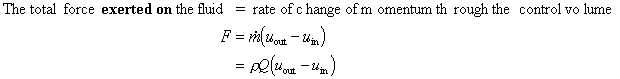
Remember that we are working with vectors so F is in the direction of the velocity. This force is made up of three components:

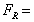Force exerted on the fluid by any solid body touching the control volume

Force exerted on the fluid body (e.g. gravity)

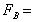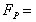Force exerted on the fluid by fluid pressure outside the control volume

So we say that the total force, F_T, is given by the sum of these forces:

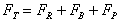
The force exerted by the fluid on the solid body touching the control volume is opposite to 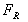. So the reaction force, R, is given by