Appendix A Various formulations of the Uniform Flow Equations

This appendix demonstrates some of the various formulations of the equations of uniform flow in an open channel.

There are a lot of equations in this document. Only the first 4 should be committed to memory. All of the others are derived from these 4 and you should become confident that you follow how they are obtained.

Refer to caption — Figure A.1: A general section of a channel with notation

The equations take the basic parameters $Q=$ flow (discharge), $V=$ velocity, $y=$ depth, $A=$ cross-sectional Area, $B=$ surface width, $P=$ wetted perimeter and $S_{o}=$ bed slope.

The Uniform Flow Equations

The Chezy Equation

The fundamental equation is the Chezy equation where $C$ is the "Chezy $C$ ":

	$\displaystyle V$	$\displaystyle=C\sqrt{RS_{o}}$
		$\displaystyle=CR^{1/2}S_{o}^{1/2}$		(A.1)

And in terms of flow (discharge)

	$\displaystyle Q$	$\displaystyle=AC\sqrt{RS_{o}}$
		$\displaystyle=ACR^{1/2}S_{o}^{1/2}$		(A.2)

The Manning’s equation

The Chezy $C$ and Manning’s $n$ are related by:

C=\frac{R^{1/6}}{n}

(A.3)

So equation A.2 becomes

	$\displaystyle Q$	$\displaystyle=\frac{1}{n}AR^{1/6}\sqrt{RS_{o}}$
		$\displaystyle=\frac{1}{n}AR^{2/3}S_{o}^{1/2}$		(A.4)

In terms of $A$ and $P$

Chezy : substituting for $R=\frac{A}{P}$ Equation A.2 becomes

$\displaystyle Q$	$\displaystyle=AC\sqrt{\frac{AS_{o}}{P}}$
	$\displaystyle=AC{\frac{A}{P}}^{1/2}S_{o}^{1/2}$
	$\displaystyle=C\frac{A^{3/2}}{P^{1/2}}S_{o}^{1/2}$
	$\displaystyle=CA^{3/2}{P}^{-1/2}S_{o}^{1/2}$	(A.5)

Manning : substituting for $R=\frac{A}{P}$ Equation A.4 becomes

$\displaystyle Q$	$\displaystyle=\frac{1}{n}A\left(\frac{A}{P}\right)^{1/6}\sqrt{\frac{A}{P}S_{o}}$
	$\displaystyle=\frac{1}{n}A\left(\frac{A}{P}\right)^{2/3}S_{o}^{1/2}$
	$\displaystyle=\frac{1}{n}\frac{A^{5/3}}{P^{2/3}}S_{o}^{1/2}$
	$\displaystyle=\frac{1}{n}A^{5/3}P^{-2/3}S_{o}^{1/2}$	(A.6)

Channels of Common Geometry

There are a few cross-sections that are very commonly constructed i.e. rectangular, trapezoidal and circular. You should be familiar with the development of the equation of uniform flow for these. Do not rely on remembering them, it is much easier to derive them from the Chezy (A.2) or Manning (A.4) generic equations.

These equations are expressions in terms of depth of flow $y_{n}$ . This depth is referred to as the normal depth. Do remember that the depth of flow in a uniform flow equation is normal depth - it is the depth that a long channel would naturally reach as gravitational and frictional forces balance.

Rectangular Channels

For a rectangular channel, we have:

A=by

and

P=b+2y

R=\frac{A}{P}=\frac{by}{b+2y}

The Chezy equation, eqn A.2 for a rectangular channel becomes:

Q=Cby_{n}\left(\frac{by_{n}}{b+2y_{n}}\right)^{1/2}S_{o}^{1/2}

(A.7)

The Manning equation, eqn A.4 for a rectangular channel becomes:

Q=\frac{1}{n}\frac{(by_{n})^{5/3}}{(b+2y_{n})^{2/3}}S_{o}^{1/2}

(A.8)

Trapezoidal Channels

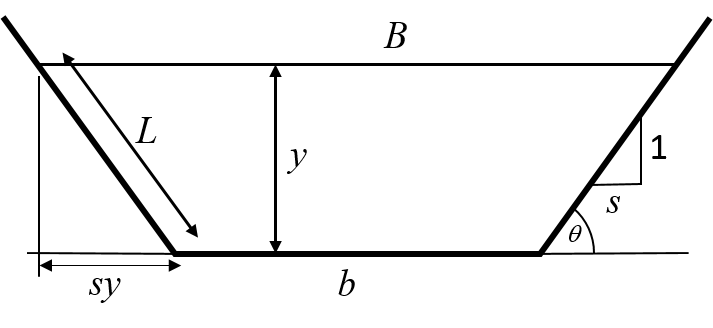
For a trapezoidal channel with base $b$ and side slopes of $1$ vertical : $s$ horizontal, then we have:

A=y(b+ys)

The wetted side slope, $L$ given by:

	$\displaystyle L$	$\displaystyle=\sqrt{y^{2}+(ys)^{2}}$
		$\displaystyle=y(1+s^{2})^{1/2}$

Thus the wetted perimeter is

	$\displaystyle P$	$\displaystyle=b+2L$
		$\displaystyle=b+2y(1+s^{2})^{1/2}$

Thus

R=\frac{y(b+ys)}{b+2y(1+s^{2})^{1/2}}

And the top width

B=b+2ys

The Chezy equation, eqn A.2 for a trapezoidal channel becomes:

Q=Cy_{n}(b+y_{n}s)\left(\frac{y_{n}(b+y_{n}s)}{b+2y_{n}(1+s^{2})^{1/2}}\right)% ^{1/2}S_{o}^{1/2}

(A.9)

The Manning equation, eqn A.4 for a trapezoidal channel becomes:

Q=\frac{1}{n}\frac{[y_{n}(b+y_{n}s)]^{5/3}}{[b+2y_{n}(1+s^{2})^{1/2}]^{2/3}}S_% {o}^{1/2}

(A.10)

Circular Channels

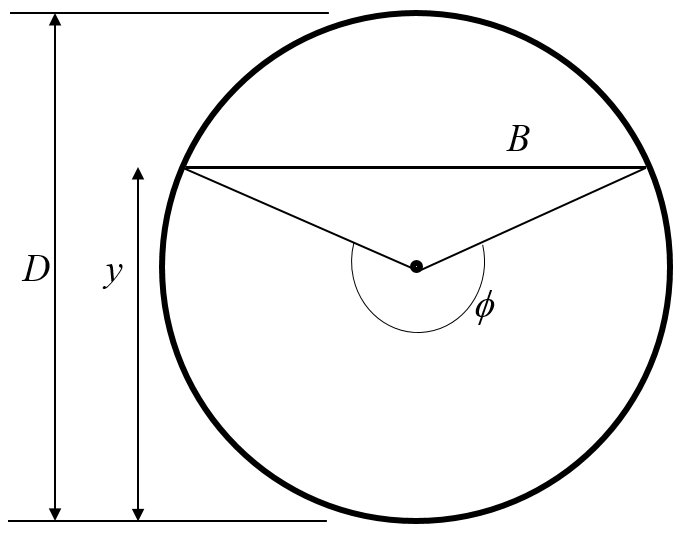
Circular channels a pipes that are not full (or just full so at atmospheric pressure).

A=\frac{D^{2}}{8}(\phi-\sin\phi)

and

P=\frac{\phi D}{2}

R=\frac{A}{P}=\frac{D}{4}\left(1-\frac{\sin\phi}{\phi}\right)

(Remember that in the above expressions $\phi$ is expressed in radians)

The Chezy equation, eqn A.2 for channel of circular section becomes:

	$\displaystyle Q$	$\displaystyle=C\frac{D^{2}}{8}(\phi-\sin\phi)\frac{D^{1/2}}{2}\left(1-\frac{% \sin\phi}{\phi}\right)^{1/2}S_{o}^{1/2}$
		$\displaystyle=C\frac{D^{5/2}}{16}(\phi-\sin\phi)\left(1-\frac{\sin\phi}{\phi}% \right)^{1/2}S_{o}^{1/2}$		(A.11)

The Manning equation, eqn A.4 for a channel of circular section becomes:

Q=\frac{1}{n}\frac{D^{2}}{8}(\phi-\sin\phi)\left[\frac{D}{4}\left(1-\frac{\sin% \phi}{\phi}\right)\right]^{2/3}S_{o}^{1/2}

(A.12)

Which could be simplified in several ways, e.g.

Q=\frac{1}{n}\frac{D^{8/3}}{20.16}(\phi-\sin\phi)\left[\left(1-\frac{\sin\phi}% {\phi}\right)\right]^{2/3}S_{o}^{1/2}

These equations are solved for $\phi$ and $y_{n}$ calculated from

y_{n}=\frac{D}{2}\left(1-\cos\frac{\phi}{2}\right)

Wide Rectangular Channels

For a wide rectangular channel we can look at the equation for $R$ again. For a rectangular channel, we have:

R=\frac{By}{B+2y}

Dividing the top and bottom by $B$ gives

R=\frac{y}{1+\frac{2y}{B}}

As $B\to\infty$ then $\frac{2y}{B}\to 0$ therefore $R\to y$ .
So for a wide rectangular channel, when $B\gg y$ , we can justifiably say:

R\approx y

(A.13)

The Chezy equation, eqn A.2 for a wide channel becomes:

	$\displaystyle Q$	$\displaystyle=By_{n}Cy_{n}^{1/2}S_{o}^{1/2}$
		$\displaystyle=CBy_{n}^{3/2}S_{o}^{1/2}$		(A.14)

The Manning equation, eqn A.4 for a wide channel becomes:

	$\displaystyle Q$	$\displaystyle=\frac{1}{n}By_{n}y_{n}^{1/6}y_{n}^{1/2}S_{o}^{1/2}$
		$\displaystyle=\frac{1}{n}By_{n}^{5/3}S_{o}^{1/2}$		(A.15)

Unit Discharge

Sometimes it is useful to quote flows in flow per unit width. Which would be in the SI system flow per $m$ . This is usually given the symbol of lowercase $q$ . It is thus defied:

\text{unit discharge }=q=\frac{Q}{B}

(A.16)

The corresponding uniform floe equations are thus equation A.7 or A.8 divided by top wide $B$ :

Chezy equation for unit discharge:

q=Cy^{3/2}S_{o}^{1/2}

(A.17)

Manning equation for unit discharge:

\displaystyle q=\frac{1}{n}y^{5/3}S_{o}^{1/2}

(A.18)

Normal depth in terms of Unit Discharge

An explicit equation for normal depth can be written from the Chezy equation A.17:

y_{n}=\sqrt[3]{\frac{q^{2}}{C^{2}S_{o}}}

(A.19)

And similarly for normal depth can be written from the Manning’s form A.18:

y_{n}=\left(\frac{qn}{S_{o}^{1/2}}\right)^{3/5}

(A.20)

Fr and Critical depth in terms of Unit Discharge

While we are discussing unit discharge, it might be worth thinking about how the Froude number, Fr, would be defined in terms of $q$ . Remembering the equation for Fr is $Fr=\frac{V}{\sqrt{gD_{m}}}$ and that $D_{m}=\frac{A}{B}$ then considering a rectangular channel and unit discharge:

V=\frac{Q}{A}=\frac{Q}{by}=\frac{q}{y}

D_{m}=\frac{A}{B}=\frac{By}{B}=y

and

Fr=\frac{q}{y}\frac{1}{g^{1/2}y^{1/2}}=\frac{q}{g^{1/2}y^{3/2}}

(A.21)

And as critical depth, $y_{c}$ , is calculated by equating $Fr$ to 1, thus

1=\frac{q}{g^{1/2}y_{c}^{3/2}}

and

y_{c}^{3/2}=\frac{q}{g^{1/2}}

y_{c}=\sqrt[3]{\frac{q^{2}}{g}}=\left(\frac{q^{2}}{g}\right)^{1/3}

(A.22)

A note on the units of Chezy $C$ and Manning $n$

Although the values of $C$ and $n$ are often quoted without units they do have units.

The units of $C$ are $m^{1/2}/s$ , or $m^{1/2}s^{-1}$ .

The units of $n$ are $s/m^{1/3}$ or $s\;m^{-1/3}$ .

Unusually (but conveniently), though $n$ has units, the value is always quoted in SI units but can be used in other systems of units. This is achieved by changing the Manning equation for that particular unit system.

Specifically for the system of English units or imperial units or, more commonly now, US customary units, or even the $FPS$ ¹¹ 1 Foot, Pound, Second system, where length is expressed in unit of $ft$ and discharge in $ft^{3}/s$ , then the Manning equation, eqn A.4 is written:

\displaystyle Q=\frac{1.49}{n}AR^{2/3}S_{o}^{1/2}

(A.23)

where the $1.49$ is a factor that conveniently converts the units of the $n$ given in SI.
(For reference, $(1m)^{1/3}/s=(3.2808399ft)^{1/3}/s=1.4859ft^{1/3}/s$ ).

Having said that these are the units of $n$ ; they are indeed the units that balance the equation. However, if we look at the units physically we see that $n$ , which is a roughness measure, is a function of time. It is unlikely that, physically, in a steady-state equation of flow, roughness changes with time. Some texts take this thought further and say that $n$ is in fact dimensionless and that the factor $1$ in SI and $1.49$ are in fact not pure numbers but dimensional constants, with units of $m^{1/3}/s$ , (or $ft^{1/3}/s$ ).