6 Examples
\setenumerate[1]label=E6.0.0.
6.1 Examples: Units
-
1.
A water company wants to check that it will have sufficient water if there is a prolonged drought in the area. The region it covers is 500 square miles and the following consumption figures have been sent in by various different offices. There is sufficient information to calculate the amount of water available, but unfortunately it is in several different units.
Of the total area 100 000 acres is rural land and the rest urban. The density of the urban population is50 per square kilometre. The average toilet cistern is sized 200mm by 15in by 0.3m and on average each person uses this 3 time per day. The density of the rural population is 5 per square mile. Baths are taken twice a week by each person with the average volume of water in the bath being 6 gallons. Local industry uses 1000 m3 per week. Other uses are estimated as 5 gallons per person per day. A US air base in the region has given water use figures of 50 US gallons per person per day.
The average rain fall in 1in per month (28 days). In the urban area all of this goes to the river while in the rural area goes to the river is lost (to the aquifer) and the rest goes to the one reservoir which supplies the region. This reservoir has an average surface area of 500 acres and is at a depth of 10 fathoms. of this volume can be used in a month.
-
(a)
What is the total consumption of water per day?
-
(b)
If the reservoir was empty and no water could be taken from the river, would there be enough water if available if rain fall was only of average?
-
(a)
6.2 Examples: Fluid Properties
-
1.
Explain why the viscosity of a liquid decreases while that of a gas increases with a temperature rise. The following is a table of measurement for a fluid at constant temperature.
Determine the dynamic viscosity of the fluid.
0.0 0.2 0.4 0.6 0.8 0.0 1.0 1.9 3.1 4.0 -
2.
The density of an oil is 850 kg/m3. Find its relative density and Kinematic viscosity if the dynamic viscosity is .
-
3.
The velocity distribution of a viscous liquid (dynamic viscosity ) flowing over a fixed plate is given by ( is velocity in and is the distance from the plate in ).
What are the shear stresses at the plate surface and at ?
-
4.
of oil weighs . Find its mass density, and relative density, .
-
5.
From table of fluid properties the viscosity of water is given as 0.01008 poises.
What is this value in and units?
-
6.
In a fluid the velocity measured at a distance of 75mm from the boundary is . The fluid has absolute viscosity and relative density 0.913. What is the velocity gradient and shear stress at the boundary assuming a linear velocity distribution?
6.3 Examples: Fluids Statics
Pressure and Manometers
-
1.
What will be the (a) the gauge pressure and (b) the absolute pressure of water at depth 12m below the surface?
, and .
[Ans: , ] -
2.
At what depth below the surface of oil, relative density 0.8, will produce a pressure of ? What depth of water is this equivalent to?
[Ans: , ] -
3.
What would the pressure in be if the equivalent head is measured as of (a) mercury (b) water ( c) oil specific weight (d) a liquid of density ?
[Ans: , , , ] -
4.
A manometer connected to a pipe indicates a negative gauge pressure of of mercury. What is the absolute pressure in the pipe in Newtons per square metre if the atmospheric pressure is 1 bar?
[Ans: ] -
5.
What height would a water barometer need to be to measure atmospheric pressure of 1 bar?
[Ans: ] -
6.
An inclined manometer is required to measure an air pressure of 3mm of water to an accuracy of . The inclined arm is in diameter and the larger arm has a diameter of . The manometric fluid has density and the scale may be read to .
What is the angle required to ensure the desired accuracy may be achieved?
[Ans: ] -
7.
Determine the resultant force due to the water acting on the 1m by 2m rectangular area AB shown in the figure 105 below.
[, from O]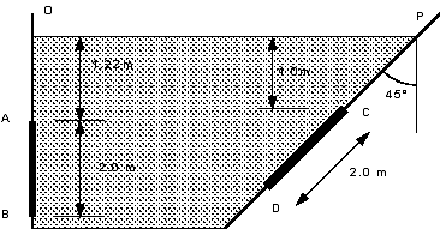
Figure 105: Tank with sloping side and gates. -
8.
Determine the resultant force due to the water acting on the 1.25m by 2.0m triangular area CD shown in the figure 105 above. The apex of the triangle is at C.
[Ans: , from P]
Forces on submerged surfaces
-
9.
Obtain an expression for the depth of the centre of pressure of a plane surface wholly submerged in a fluid and inclined at an angle to the free surface of the liquid.
A horizontal circular pipe, diameter, is closed by a butterfly disk which rotates about a horizontal axis through its centre. Determine the torque which would have to be applied to the disk spindle to keep the disk closed in a vertical position when there is a 3m head of fresh water above the axis.
[Ans: 1176 Nm] -
10.
(HARDER) A dock gate is to be reinforced with three horizontal beams. If the water acts on one side only, to a depth of , find the positions of the beams measured from the water surface so that each will carry an equal load. Give the load per meter.
[Ans: , , , ] -
11.
The profile of a masonry dam is an arc of a circle, the arc having a radius of and subtending an angle of at the centre of curvature which lies in the water surface. Determine (a) the load on the dam in length, (b) the position of the line of action to this pressure.
[Ans: length at depth ] -
12.
(HARDER) The arch of a bridge over a stream is in the form of a semi-circle of radius . the bridge width is . Due to a flood the water level is now above the crest of the arch. Calculate (a) the upward force on the underside of the arch, (b) the horizontal thrust on one half of the arch.
[Ans: , ] -
13.
The face of a dam is vertical to a depth of below the water surface then slopes at to the vertical. If the depth of water is what is the resultant force per metre acting on the whole face?
[Ans: ] -
14.
A tank with vertical sides is square in plan with long sides. The tank contains oil of relative density 0.9 to a depth of which is floating on water a depth of . Calculate the force on the walls and the height of the centre of pressure from the bottom of the tank.
[Ans: , ]
6.4 Examples: Fluid Dynamics: Bernoulli Equation
Application of the Bernoulli Equation
-
1.
In a vertical pipe carrying water, pressure gauges are inserted at points A and B where the pipe diameters are 0.15m and 0.075m respectively. The point B is 2.5m below A and when the flow rate down the pipe is 0.02 cumecs, the pressure at B is greater than that at A.
Assuming the losses in the pipe between A and B can be expressed as where is the velocity at A, find the value of .
If the gauges at A and B are replaced by tubes filled with water and connected to a U-tube containing mercury of relative density 13.6, give a sketch showing how the levels in the two limbs of the U-tube differ and calculate the value of this difference in metres.
[Ans: , ] -
2.
A Venturimeter with an entrance diameter of 0.3m and a throat diameter of 0.2m is used to measure the volume of gas flowing through a pipe. The discharge coefficient of the meter is 0.96. Assuming the specific weight of the gas to be constant at , calculate the volume flowing when the pressure difference between the entrance and the throat is measured as 0.06m on a water U-tube manometer. [Ans: ]
-
3.
A Venturimeter is used for measuring flow of water along a pipe. The diameter of the Venturi throat is two fifths the diameter of the pipe. The inlet and throat are connected by water filled tubes to a mercury U-tube manometer. The velocity of flow along the pipe is found to be , where is the manometer reading in metres of mercury. Determine the loss of head between inlet and throat of the Venturi when is . (Relative density of mercury is 13.6).
[Ans: of water] -
4.
(HARDER) Water is discharging from a tank through a convergent-divergent mouthpiece. The exit from the tank is rounded so that losses there may be neglected and the minimum diameter is 0.05m.
If the head in the tank above the centre-line of the mouthpiece is 1.83m. a) What is the discharge? b) What must be the diameter at the exit if the absolute pressure at the minimum area is to be 2.44m of water? c) What would the discharge be if the divergent part of the mouth piece were removed. (Assume atmospheric pressure is 10m of water).
[Ans: , , ] -
5.
(HARDER) A closed tank has an orifice 0.025m diameter in one of its vertical sides. The tank contains oil to a depth of 0.61m above the centre of the orifice and the pressure in the air space above the oil is maintained at above atmospheric. Determine the discharge from the orifice.
(Coefficient of discharge of the orifice is 0.61, relative density of oil is 0.9).
[Ans: ] -
6.
(HARDER) The discharge coefficient of a Venturimeter was found to be constant for rates of flow exceeding a certain value. Show that for this condition the loss of head due to friction in the convergent parts of the meter can be expressed as where is a constant and is the rate of flow in cumecs.
Obtain the value of if the inlet and throat diameter of the Venturimeter are 0.102m and 0.05m respectively and the discharge coefficient is 0.96.
[Ans: ] -
7.
A Venturimeter is to fitted in a horizontal pipe of 0.15m diameter to measure a flow of water which may be anything up to . The pressure head at the inlet for this flow is 18m above atmospheric and the pressure head at the throat must not be lower than 7m below atmospheric. Between the inlet and the throat there is an estimated frictional loss of 10% of the difference in pressure head between these points. Calculate the minimum allowable diameter for the throat.
[Ans: ] -
8.
A Venturimeter of throat diameter 0.076m is fitted in a 0.152m diameter vertical pipe in which liquid of relative density 0.8 flows downwards. Pressure gauges are fitted to the inlet and to the throat sections. The throat being 0.914m below the inlet. Taking the coefficient of the meter as 0.97 find the discharge a) when the pressure gauges read the same b)when the inlet gauge reads higher than the throat gauge.
[Ans: , ]
Tank emptying
-
1.
(HARDER) A reservoir is circular in plan and the sides slope at an angle of to the horizontal. When the reservoir is full the diameter of the water surface is 50m. Discharge from the reservoir takes place through a pipe of diameter 0.65m, the outlet being 4m below top water level. Determine the time for the water level to fall 2m assuming the discharge to be cumecs where is the cross sectional area of the pipe in and is the head of water above the outlet in .
[Ans: ] -
2.
(HARDER) A rectangular swimming pool is 1m deep at one end and increases uniformly in depth to 2.6m at the other end. The pool is 8m wide and 32m long and is emptied through an orifice of area , at the lowest point in the side of the deep end. Taking Cd for the orifice as 0.6, find, from first principles, a) the time for the depth to fall by 1m b) the time to empty the pool completely.
[Ans: , ] -
3.
A vertical cylindrical tank 2m diameter has, at the bottom, a 0.05m diameter sharp edged orifice for which the discharge coefficient is 0.6.
a) If water enters the tank at a constant rate of 0.0095 cumecs find the depth of water above the orifice when the level in the tank becomes stable. b) Find the time for the level to fall from 3m to 1m above the orifice when the inflow is turned off. c) If water now runs into the tank at 0.02 cumecs, the orifice remaining open, find the rate of rise in water level when the level has reached a depth of 1.7m above the orifice.
[Ans: a) , b), c) ] -
4.
(HARDER) A horizontal boiler shell (i.e. a horizontal cylinder) 2m diameter and 10m long is half full of water. Find the time of emptying the shell through a short vertical pipe, diameter 0.08m, attached to the bottom of the shell. Take the coefficient of discharge to be 0.8.
[Ans: ] -
5.
Two cylinders standing upright contain liquid and are connected by a submerged orifice. The diameters of the cylinders are 1.75m and 1.0m and of the orifice, 0.08m. The difference in levels of the liquid is initially 1.35m. Find how long it will take for this difference to be reduced to 0.66m if the coefficient of discharge for the orifice is 0.605. (Work from first principles.)
[Ans: ] -
6.
A rectangular reservoir with vertical walls has a plan area of . Discharge from the reservoir take place over a rectangular weir. The flow characteristics of the weir is cumecs where is the depth of water above the weir crest. The sill of the weir is 3.4m above the bottom of the reservoir. Starting with a depth of water of 4m in the reservoir and no inflow, what will be the depth of water after one hour?
[Ans: ]Notches and weirs
-
7.
Deduce an expression for the discharge of water over a right-angled sharp edged V-notch, given that the coefficient of discharge is 0.61.
A rectangular tank 16m by 6m has the same notch in one of its short vertical sides. Determine the time taken for the head, measured from the bottom of the notch, to fall from 15cm to 7.5cm.
[Ans: ] -
8.
Derive an expression for the discharge over a sharp crested rectangular weir. A sharp edged weir is to be constructed across a stream in which the normal flow is . If the maximum flow likely to occur in the stream is 5 times the normal flow then determine the length of weir necessary to limit the rise in water level to 38.4cm above that for normal flow. .
[Ans: ] -
9.
Show that the rate of flow across a triangular notch is given by cumecs, where is an experimental coefficient, depends on the angle of the notch, and H is the height of the undisturbed water level above the bottom of the notch in metres. State the reasons for the introduction of the coefficient. Water from a tank having a surface area of flows over a notch. It is found that the time taken to lower the level from 8cm to 7cm above the bottom of the notch is 43.5 seconds. Determine the coefficient assuming that it remains constant during his period.
[Ans: ] -
10.
A reservoir with vertical sides has a plan area of 56000m2. Discharge from the reservoir takes place over a rectangular weir, the flow characteristic of which is . At times of maximum rainfall, water flows into the reservoir at the rate of . Find a) the length of weir required to discharge this quantity if head must not exceed 0.6m; b) the time necessary for the head to drop from 60cm to 30cm if the inflow suddenly stops.
[Ans: , ] -
11.
Develop a formula for the discharge over a V-notch weir in terms of head above the bottom of the V. A channel conveys of water. At the outlet end there is a V-notch weir for which the coefficient of discharge is 0.58. At what distance above the bottom of the channel should the weir be placed in order to make the depth in the channel 1.30m? With the weir in this position what is the depth of water in the channel when the flow is ?
[Ans: , ] -
12.
Show that the quantity of water flowing across a triangular V-notch of angle is
Find the flow if the measured head above the bottom of the V is 38cm, when and . If the flow is wanted within an accuracy of 2%, what are the limiting values of the head.
[Ans: , , ]
6.5 Examples: Fluid Dynamics: Momentum Equation
-
1.
The figure below shows a smooth curved vane attached to a rigid foundation. The jet of water, rectangular in section, wide and thick, strike the vane with a velocity of . Calculate the vertical and horizontal components of the force exerted on the vane and indicate in which direction these components act.
[Ans: Horizontal acting from right to left. Vertical acting downwards] -
2.
A diameter pipeline carries water under a head of with a velocity of . This water main is fitted with a horizontal bend which turns the axis of the pipeline through (i.e. the internal angle at the bend is ). Calculate the resultant force on the bend and its angle to the horizontal.
[Ans: , ] -
3.
A horizontal jet of water cross-section and flowing at a velocity of hits a flat plate at to the axis (of the jet) and to the horizontal. The jet is such that there is no side spread. If the plate is stationary, calculate a) the force exerted on the plate in the direction of the jet and b) the ratio between the quantity of fluid that is deflected upwards and that downwards. (Assume that there is no friction and therefore no shear force.)
[Ans: 338N, 3:1] -
4.
A diameter jet of water having a velocity of strikes a flat plate, the normal of which is inclined at to the jet. Find the force normal to the surface of the plate.
[Ans: 2.39kN] -
5.
The outlet pipe from a pump is a bend of rising in the vertical plane (i.e. and internal angle of ). The bend is diameter at its inlet and diameter at its outlet. The pipe axis at the inlet is horizontal and at the outlet it is higher. By neglecting friction, calculate the force and its direction if the inlet pressure is and the flow of water through the pipe is . The volume of the pipe is .
[Ans: 13.94kN at 67? 40’ to the horizontal] -
6.
The force exerted by a diameter jet against a flat plate normal to the axis of the jet is . What is the flow in ?
[Ans: ] -
7.
A curved plate deflects a diameter jet through an angle of . For a velocity in the jet of to the right, compute the components of the force developed against the curved plate. (Assume no friction).
[Ans: , down] -
8.
A reducing bend, diameter upstream, diameter downstream, has water flowing through it at the rate of under a pressure of . Neglecting any loss is head for friction, calculate the force exerted by the water on the bend, and its direction of application.
[Ans: to the right and down, ]
6.6 Example: Boundary Effects: Laminar Flow
-
1.
The distribution of velocity, , in with radius in , in a smooth bore tube of bore follows the law, . Where is a constant. The flow is laminar and the velocity at the pipe surface is zero. The fluid has a coefficient of viscosity of . Determine (a) the rate of flow in (b) the shearing force between the fluid and the pipe wall per metre length of pipe.
[Ans: , ] -
2.
A liquid whose coefficient of viscosity is flows below the critical velocity for laminar flow in a circular pipe of diameter and with mean velocity . Show that the pressure loss in a length of pipe is . Oil of viscosity flows through a pipe of diameter with a velocity of . Calculate the loss of pressure in a length of .
[Ans: ] -
3.
(HARDER)A plunger of diameter and length has four small holes of diameter drilled through in the direction of its length. The plunger is a close fit inside a cylinder, containing oil, such that no oil is assumed to pass between the plunger and the cylinder. If the plunger is subjected to a vertical downward force of (including its own weight) and it is assumed that the upward flow through the four small holes is laminar, determine the speed of the fall of the plunger. The coefficient of viscosity of the oil is .
[Ans: ] -
4.
A vertical cylinder of diameter is mounted concentrically in a drum of internal diameter. Oil fills the space between them to a depth of . The torque required to rotate the cylinder in the drum is when the speed of rotation is . Assuming that the end effects are negligible, calculate the coefficient of viscosity of the oil.
[Ans: ]