3 Forces in Static Fluids
This section will study the forces acting on or generated by fluids at rest.
Objectives
-
•
Introduce the concept of pressure;
-
•
Prove it has a unique value at any particular elevation;
-
•
Show how it varies with depth according to the hydrostatic equation and
-
•
Show how pressure can be expressed in terms of head of fluid.
This understanding of pressure will then be used to demonstrate methods of pressure measurement that will be useful later with fluid in motion and also to analyse the forces on submerged surface/structures.
3.1 Fluids statics
The general rules of statics (as applied in solid mechanics) apply to fluids at rest. From earlier we know that:
-
i.
A static fluid can have no shearing force acting on it, and that
-
ii.
Any force between the fluid and the boundary must be acting at right angles to the boundary.
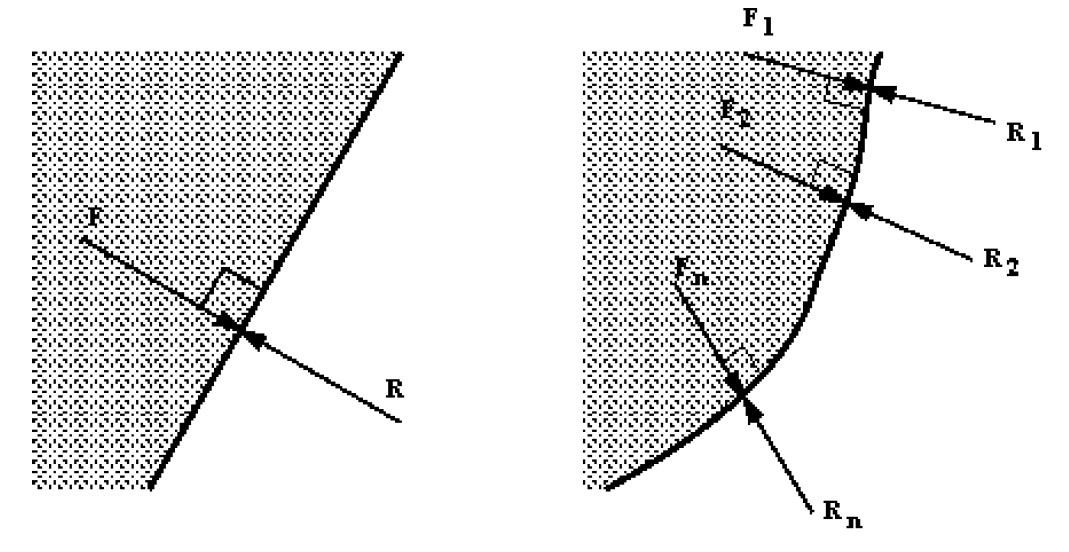
Note that this statement is also true for curved surfaces, in this case the force acting at any point is normal to the surface at that point. The statement is also true for any imaginary plane in a static fluid. We use this fact in our analysis by considering elements of fluid bounded by imaginary planes.
We also know that:
-
i.
For an element of fluid at rest, the element will be in equilibrium - the sum of the components of forces in any direction will be zero.
-
ii.
The sum of the moments of forces on the element about any point must also be zero.
It is common to test equilibrium by resolving forces along three mutually perpendicular axes and also by taking moments in three mutually perpendicular planes an to equate these to zero.
3.2 Pressure
As mentioned above a fluid will exert a normal force on any boundary it is in contact with. Since these boundaries may be large and the force may differ from place to place it is convenient to work in terms of pressure, , which is the force per unit area. If the force exerted on each unit area of a boundary is the same, the pressure is said to be uniform.
| pressure | |||
Units: Newton’s per square metre, , .
(The same unit is also known as a Pascal, , i.e. )
(Also frequently used is the alternative SI unit the bar, where )
Dimensions: .
3.3 Pascal’s Law for Pressure At A Point
(Proof that pressure acts equally in all directions.)
By considering a small element of fluid in the form of a triangular prism which contains a point , we can establish a relationship between the three pressures in the direction, in the direction and in the direction normal to the sloping face.
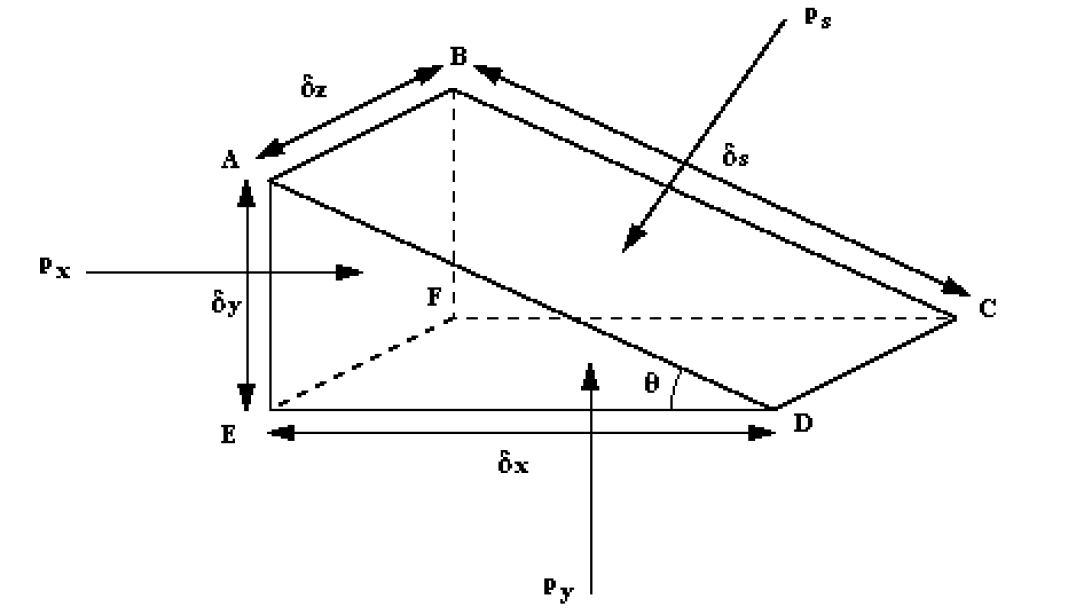
The fluid is a rest, so we know there are no shearing forces, and we know that all force are acting at right angles to the surfaces .i.e.
-
acts perpendicular to surface ABCD,
-
acts perpendicular to surface ABFE and
-
acts perpendicular to surface FECD.
And, as the fluid is at rest, in equilibrium, the sum of the forces in any direction is zero.
Summing forces in the -direction:
Force due to ,
Component of force in the x-direction due to ,
( )
Component of force in x-direction due to ,
To be at rest (in equilibrium)
Similarly, summing forces in the y-direction. Force due to ,
Component of force due to ,
Component of force due to ,
Force due to gravity,
| weight | |||
To be at rest (in equilibrium)
The element is small i.e. , and are small, and so is very small and considered negligible, hence
thus Considering the prismatic element again, is the pressure on a plane at any angle , the x, y and z directions could be any orientation. The element is so small that it can be considered a point so the derived expression . indicates that pressure at any point is the same in all directions.
(The proof may be extended to include the z axis).
Pressure at any point is the same in all directions.
This is known as Pascal’s Law and applies to fluids at rest.
3.3.1 Variation Of Pressure Vertically In A Fluid Under Gravity
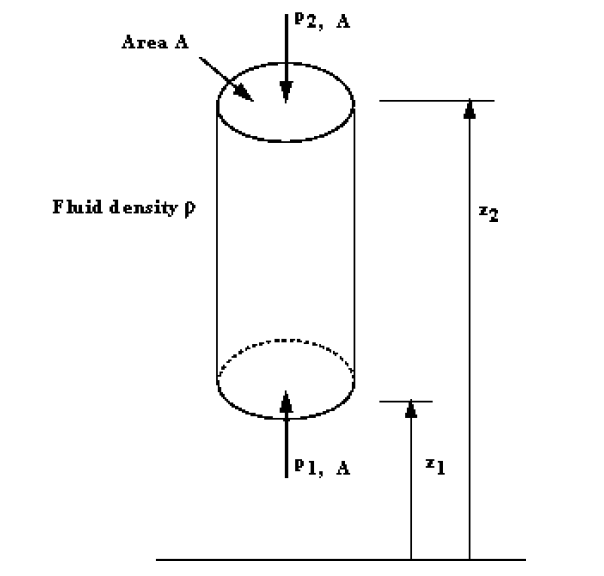
In the above figure we can see an element of fluid which is a vertical column of constant cross sectional area, A, surrounded by the same fluid of mass density . The pressure at the bottom of the cylinder is at level , and at the top is at level . The fluid is at rest and in equilibrium so all the forces in the vertical direction sum to zero. i.e. we have
| Force due to weight of element (downward) | |||
Taking upward as positive, in equilibrium we have
Thus in a fluid under gravity, pressure decreases with increase in height .
3.3.2 Equality Of Pressure At The Same Level In A Static Fluid
Consider the horizontal cylindrical element of fluid in the figure below, with cross-sectional area A, in a fluid of density , pressure at the left hand end and pressure at the right hand end.
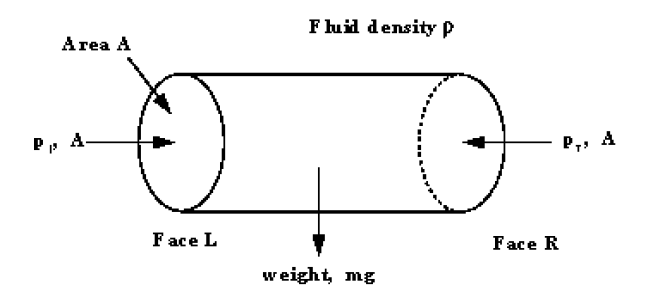
The fluid is at equilibrium so the sum of the forces acting in the x direction is zero.
Pressure in the horizontal direction is constant.
This result is the same for any continuous fluid. It is still true for two connected tanks which appear not to have any direct connection, for example consider the tank in the figure below.
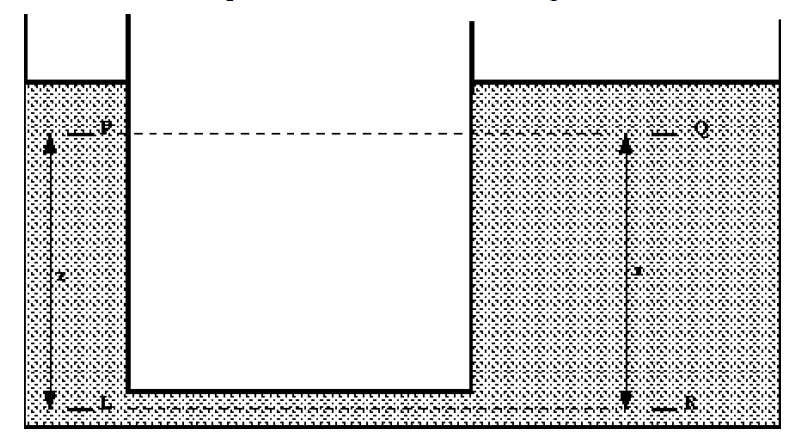
We have shown above that and from the equation for a vertical pressure change we have
and
so
This shows that the pressures at the two equal levels, P and Q are the same.
3.3.3 General Equation For Variation Of Pressure In A Static Fluid
Here we show how the above observations for vertical and horizontal elements of fluids can be generalised for an element of any orientation.
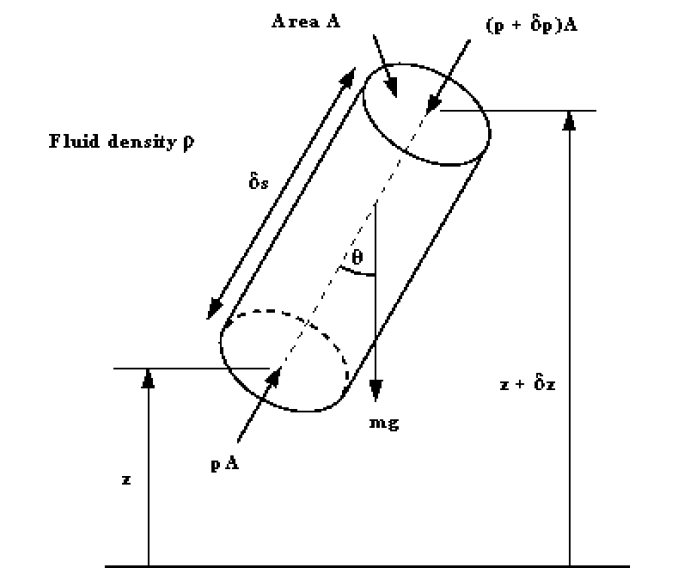
Consider the cylindrical element of fluid in the figure above, inclined at an angle to the vertical, length , cross-sectional area A in a static fluid of mass density . The pressure at the end with height is and at the end of height is .
The forces acting on the element are
There are also forces from the surrounding fluid acting normal to these sides of the element. For equilibrium of the element the resultant of forces in any direction is zero. Resolving the forces in the direction along the central axis gives
Or in the differential form
If then is in the or directions, (i.e. horizontal), so
Confirming that pressure change on any horizontal plane is zero.
If then is in the direction (vertical) so
Confirming the result
3.3.4 Pressure And Head
In a static fluid of constant density we have the relationship , as shown above. This can be integrated to give
In a liquid with a free surface the pressure at any depth measured from the free surface so that (see the figure below)
This gives the pressure
At the surface of fluids we are normally concerned with, the pressure is the atmospheric pressure, . So
As we live constantly under the pressure of the atmosphere, and everything else exists under this pressure, it is convenient (and often done) to take atmospheric pressure as the datum. So we quote pressure as above or below atmospheric.
Pressure quoted in this way is known as gauge pressure i.e.
Gauge pressure:
The lower limit of any pressure is zero - that is the pressure in a perfect vacuum. Pressure measured above this datum is known as absolute pressure i.e.
Absolute pressure:
Absolute pressure = Gauge pressure + Atmospheric pressure
As is (approximately) constant, the gauge pressure can be given by stating the vertical height of any fluid of density which is equal to this pressure.
This vertical height is known as head of fluid.
Note: If pressure is quoted in head, the density of the fluid must also be given.
Example:
We can quote a pressure of in terms of the height of a column of water of density, . Using ,
And in terms of Mercury with density, .
3.4 Pressure Measurement by Manometers
The relationship between pressure and head is used to measure pressure with a manometer (also know as a liquid gauge).
Objective:
-
1.
To demonstrate the analysis and use of various types of manometers for pressure measurement.
3.4.1 The Piezometer Tube Manometer
The simplest manometer is a tube, open at the top, which is attached to the top of a vessel containing liquid at a pressure (higher than atmospheric) to be measured. An example can be seen in the figure below. This simple device is known as a Piezometer tube. As the tube is open to the atmosphere the pressure measured is relative to atmospheric so is gauge pressure.
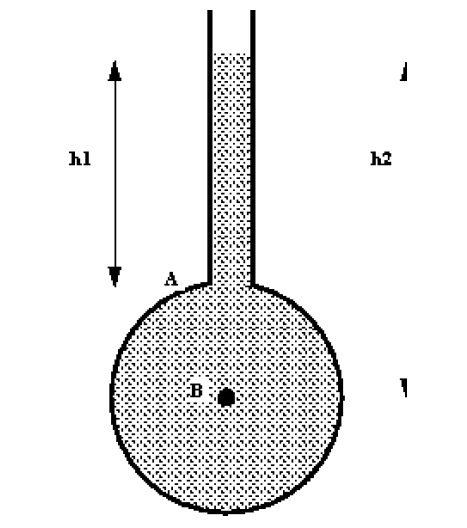
This method can only be used for liquids (i.e. not for gases) and only when the liquid height is convenient to measure. It must not be too small or too large and pressure changes must be detectable.
3.4.2 The ”U”-Tube Manometer
Using a ”U”-Tube enables the pressure of both liquids and gases to be measured with the same instrument. The ”U” is connected as in the figure below and filled with a fluid called the manometric fluid. The fluid whose pressure is being measured should have a mass density less than that of the manometric fluid and the two fluids should not be able to mix readily - that is, they must be immiscible.
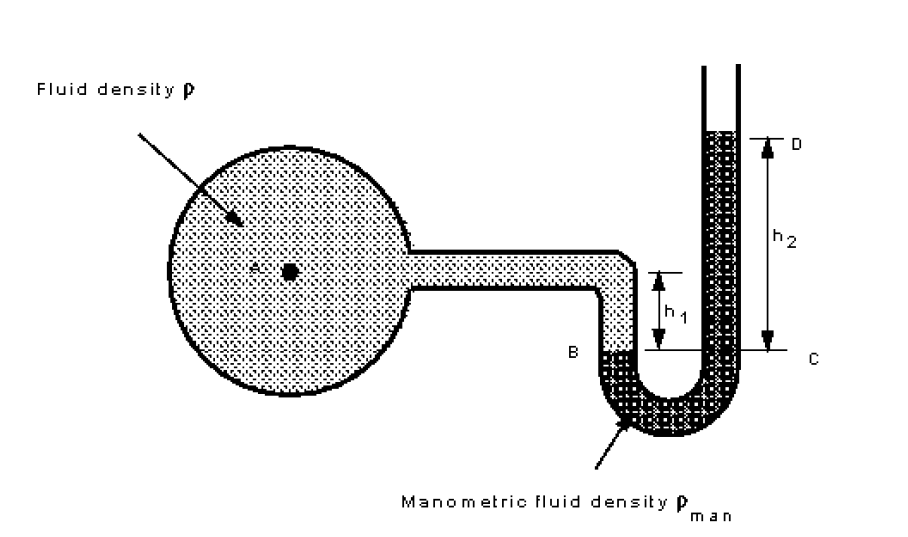
Pressure in a continuous static fluid is the same at any horizontal level so,
For the left hand arm
For the right hand arm
As we are measuring gauge pressure we can subtract giving If the fluid being measured is a gas, the density will probably be very low in comparison to the density of the manometric fluid i.e. . In this case the term can be neglected, and the gauge pressure given by
3.4.3 Measurement Of Pressure Difference Using a ”U”-Tube Manometer.
If the ”U”-tube manometer is connected to a pressurised vessel at two points the pressure difference between these two points can be measured.
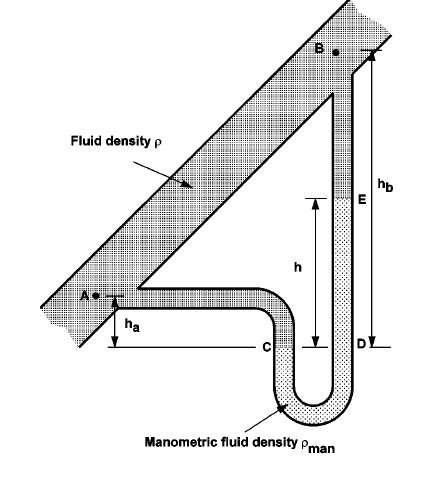
If the manometer is arranged as in the figure above, then
Giving the pressure difference Again, if the fluid whose pressure difference is being measured is a gas and , then the terms involving can be neglected, so
3.4.4 Advances to the ”U” tube manometer.
The ”U”-tube manometer has the disadvantage that the change in height of the liquid in both sides must be read. This can be avoided by making the diameter of one side very large compared to the other. In this case the side with the large area moves very little when the small area side move considerably more.
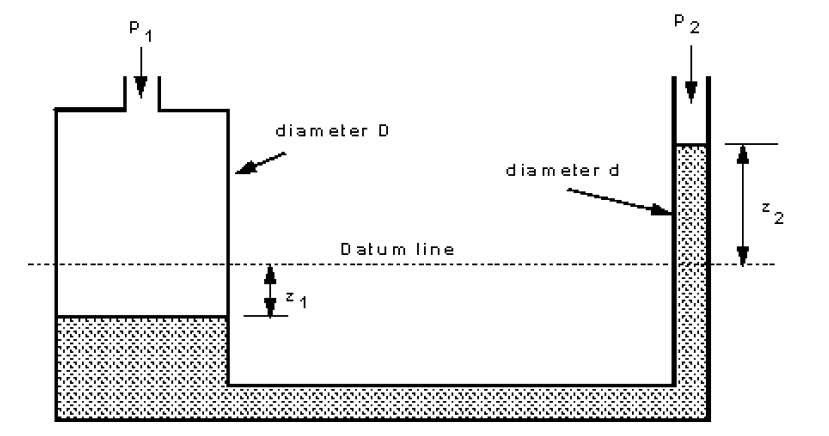
Assume the manometer is arranged as above to measure the pressure difference of a gas of (negligible density) and that pressure difference is . If the datum line indicates the level of the manometric fluid when the pressure difference is zero and the height differences when pressure is applied is as shown, the volume of liquid transferred from the left side to the right .
And the fall in level of the left side is
We know from the theory of the ”U” tube manometer that the height different in the two columns gives the pressure difference so
Clearly if is very much larger than then is very small so
So only one reading need be taken to measure the pressure difference.
If the pressure to be measured is very small then tilting the arm provides a convenient way of obtaining a larger (more easily read) movement of the manometer. The above arrangement with a tilted arm is shown in the figure below.
Tilted or Inclined manometer.
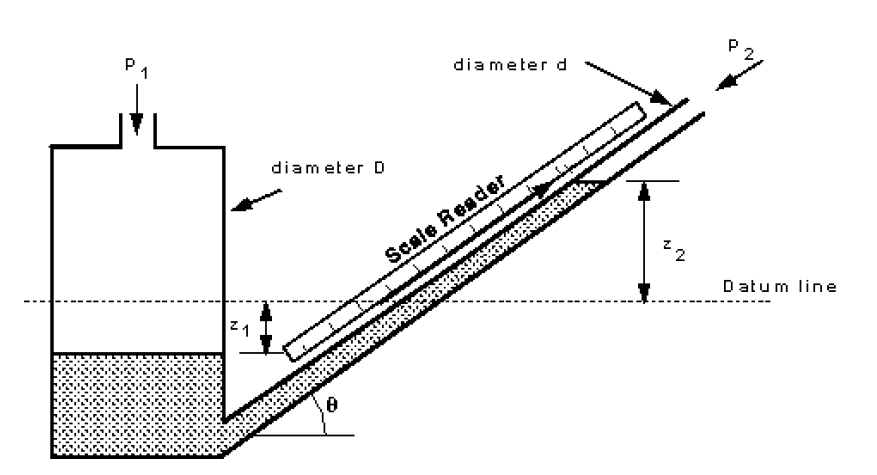
The pressure difference is still given by the height change of the manometric fluid but by placing the scale along the line of the tilted arm and taking this reading large movements will be observed. The pressure difference is then given by
The sensitivity to pressure change can be increased further by a greater inclination of the manometer arm, alternatively the density of the manometric fluid may be changed.
3.4.5 Choice Of Manometer
Care must be taken when attaching the manometer to vessel, no burrs must be present around this joint. Burrs would alter the flow causing local pressure variations to affect the measurement. Some disadvantages of manometers:
-
i
Slow response - only really useful for very slowly varying pressures - no use at all for fluctuating pressures;
-
ii
For the ”U” tube manometer two measurements must be taken simultaneously to get the h value. This may be avoided by using a tube with a much larger cross-sectional area on one side of the manometer than the other;
-
iii
It is often difficult to measure small variations in pressure - a different manometric fluid may be required - alternatively a sloping manometer may be employed; It cannot be used for very large pressures unless several manometers are connected in series;
-
iv
For very accurate work the temperature and relationship between temperature and ? must be known;
Some advantages of manometers:
-
a
They are very simple.
-
b
No calibration is required - the pressure can be calculated from first principles.
3.5 Forces on Submerged Surfaces in Static Fluids
Forces on Submerged Surfaces in Static Fluids
We have seen the following features of statics fluids
-
•
Hydrostatic vertical pressure distribution
-
•
Pressures at any equal depths in a continuous fluid are equal
-
•
Pressure at a point acts equally in all directions (Pascal’s law).
-
•
Forces from a fluid on a boundary acts at right angles to that boundary.
Objectives: We will use these to analyse and obtain expressions for the forces on submerged surfaces. In doing this it should also be clear the difference between:
-
i
Pressure which is a scalar quantity whose value is equal in all directions and,
-
ii
Force, which is a vector quantity having both magnitude and direction.
3.5.1 Fluid pressure on a surface
Pressure is defined as force per unit area. If a pressure p acts on a small area then the force exerted on that area will be
Since the fluid is at rest the force will act at right-angles to the surface.
General submerged plane Consider the plane surface shown in the figure below. The total area is made up of many elemental areas. The force on each elemental area is always normal to the surface but, in general, each force is of different magnitude as the pressure usually varies.
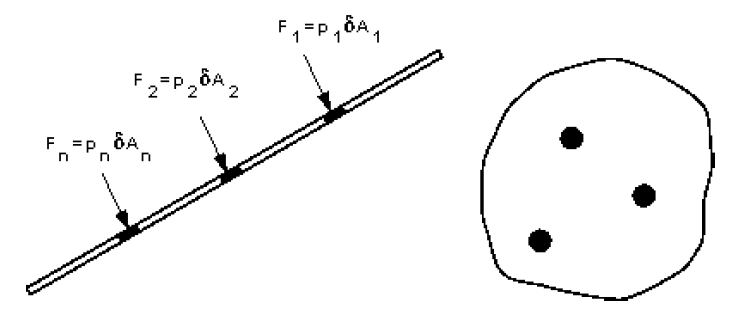
We can find the total or resultant force, , on the plane by summing up all of the forces on the small elements i.e.
This resultant force will act through the centre of pressure, hence we can say If the surface is a plane the force can be represented by one single resultant force, acting at right-angles to the plane through the centre of pressure.
Horizontal submerged plane
For a horizontal plane submerged in a liquid (or a plane experiencing uniform pressure over its surface), the pressure, , will be equal at all points of the surface. Thus the resultant force will be given by
Curved submerged surface
If the surface is curved, each elemental force will be a different magnitude and in different direction but still normal to the surface of that element. The resultant force can be found by resolving all forces into orthogonal co-ordinate directions to obtain its magnitude and direction. This will always be less than the sum of the individual forces, .
3.6 Resultant Force and Centre of Pressure on a submerged plane surface in a liquid.
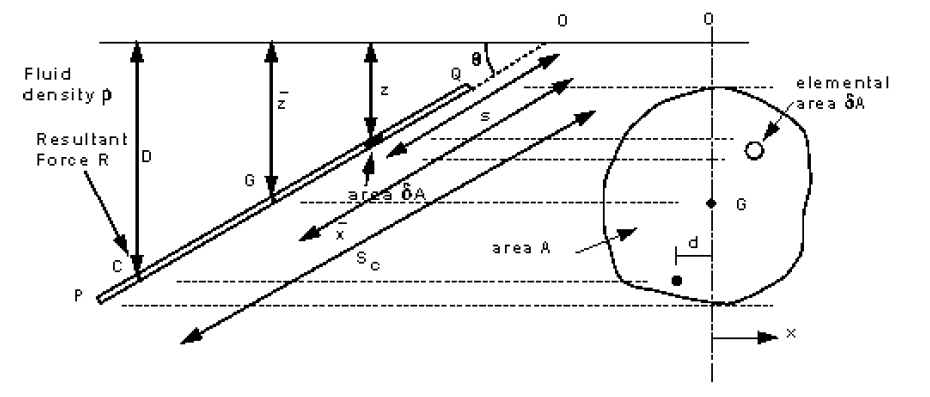
This plane surface is totally submerged in a liquid of density and inclined at an angle of to the horizontal. Taking pressure as zero at the surface and measuring down from the surface, the pressure on an element , submerged a distance , is given by
and therefore the force on the element is
The resultant force can be found by summing all of these forces i.e.
(assuming and as constant).
The term is known as the 1st Moment of Area of the plane about the free surface. It is equal to i.e.
where is the area of the plane and is the depth (distance from the free surface) to the centroid, . This can also be written in terms of distance from point (as )
Thus:
The resultant force on a plane
The resultant force on a plane
This resultant force acts at right angles to the plane through the centre of pressure, , at a depth . The moment of about any point will be equal to the sum of the moments of the forces on all the elements of the plane about the same point. We use this to find the position of the centre of pressure.
It is convenient to take moments about the point where a projection of the plane passes through the surface, point in the figure.
| Sum of moments of force | |||
We can calculate the force on each elemental area:
And the moment of this force is:
, g and are the same for each element, so the total moment is
We know the resultant force from above , which acts through the centre of pressure at C, so
Equating gives,
Thus the position of the centre of pressure along the plane measure from the point O is:
It look a rather difficult formula to calculate - particularly the summation term. Fortunately this term is known as the 2nd Moment of Area, , of the plane about the axis through and it can be easily calculated for many common shapes. So, we know:
And as we have also seen that = 1st Moment of area about a line through O,
Thus the position of the centre of pressure along the plane measure from the point O is:
and
depth to the centre of pressure is
3.6.1 How do you calculate the 2nd moment of area?
To calculate the 2nd moment of area of a plane about an axis through O, we use the parallel axis theorem together with values of the 2nd moment of area about an axis though the centroid of the shape obtained from tables of geometric properties.
The parallel axis theorem can be written
where is the 2nd moment of area about an axis through the centroid of the plane.
Using this we get the following expressions for the position of the centre of pressure
(In the examination the parallel axis theorem and the will be given)
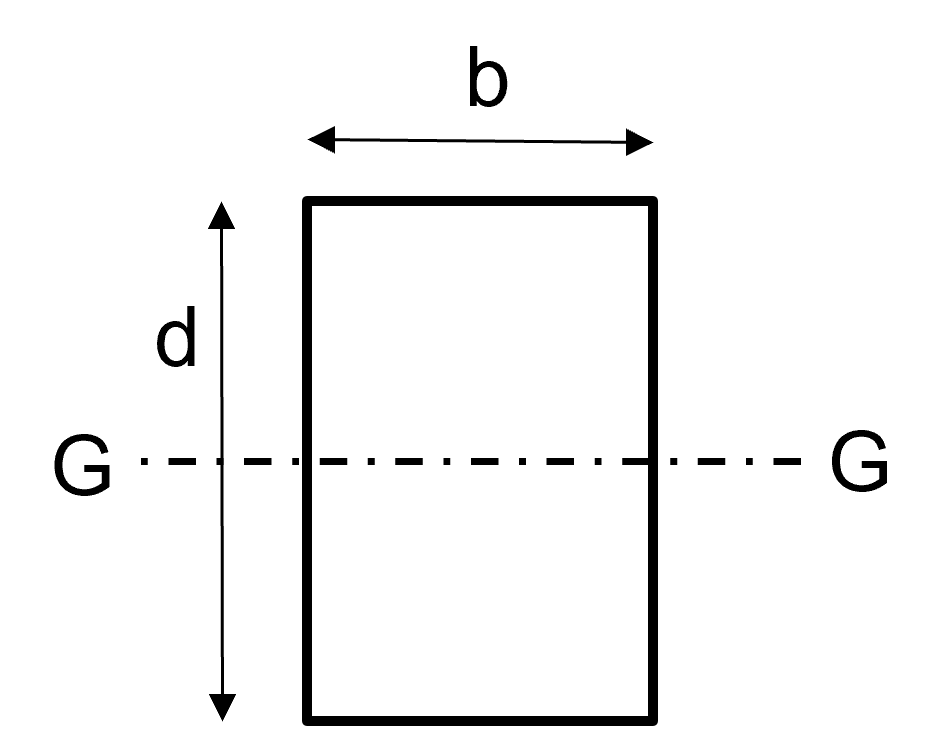
3.6.2 The second moment of area of some common shapes.
The table blow given some examples of the 2nd moment of area about a line through the centroid of some common shapes.
| Shape | Area | 2nd moment of area , |
| about an axis through the centroid | ||
| Rectangle | ||
|
||
| Triangle | ||
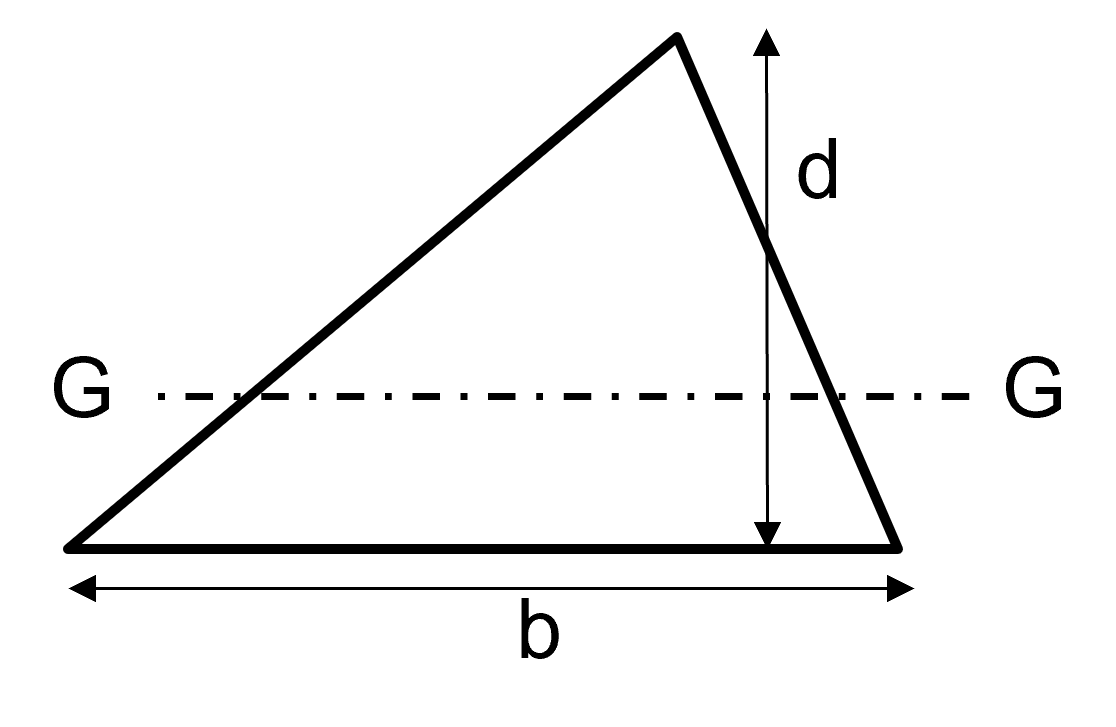
|
||
| Circle | ||
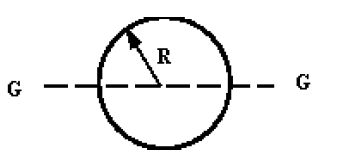
|
||
| Semi-Circle | ||
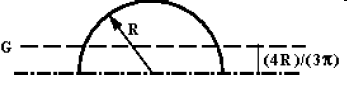
|
Lateral position of Centre of Pressure
If the shape is symmetrical the centre of pressure lies on the line of symmetry. But if it is not symmetrical its position must be found by taking moments about the line OG in the same way as we took moments along the line through O, i.e.
but we have so
3.6.3 Submerged vertical surface - Pressure diagrams
For vertical walls of constant width it is usually much easier to find the resultant force and centre of pressure. This is drawn graphically by means of a pressure diagram.
Consider the tank in the diagram below having vertical walls and holding a liquid of density to a depth of . To the right can be seen a graphical representation of the (gauge) pressure change with depth on one of the vertical walls. Pressure increases from zero at the surface linearly by , to a maximum at the base of .
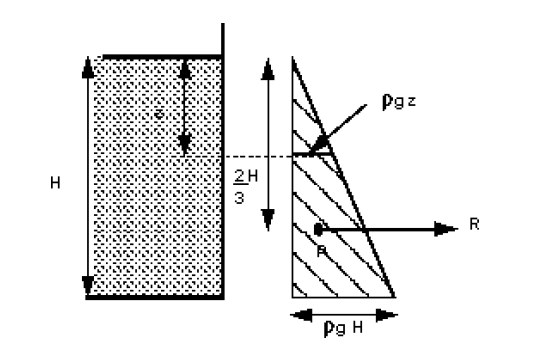
The area of this triangle represents the resultant force per unit width on the vertical wall, using SI units this would have units of Newtons per metre. So
| Area | |||
Resultant force per unit width
(N/m)
The force acts through the centroid of the pressure diagram. For a triangle the centroid is at 2/3 its height, i.e. in the figure above the resultant force acts horizontally through the point .
For a vertical plane the depth to the centre of pressure is given by
This can be checked against the previous method:
The resultant force is given by:
and the depth to the centre of pressure by:
and by the parallel axis theorem (with width of 1)
Giving depth to the centre of pressure
These two results are identical to the pressure diagram method.
The same pressure diagram technique can be used when combinations of liquids are held in tanks (e.g. oil floating on water) with position of action found by taking moments of the individual resultant forces for each fluid. Look at the examples to examine this area further.
More complex pressure diagrams can be draw for non-rectangular or non-vertical planes but it is usually far easier to use the moments method.
3.6.4 Resultant force on a submerged curved surface
As stated above, if the surface is curved the forces on each element of the surface will not be parallel and must be combined using some vectorial method.
It is most straightforward to calculate the horizontal and vertical components and combine these to obtain the resultant force and its direction. (This can also be done for all three dimensions, but here we will only look at one vertical plane).
In the diagram below the liquid is resting on top of a curved base.
The element of fluid ABC is equilibrium (as the fluid is at rest).
Horizontal forces
Considering the horizontal forces, none can act on CB as there are no shear forces in a static fluid so the forces would act on the faces AC and AB as shown below.
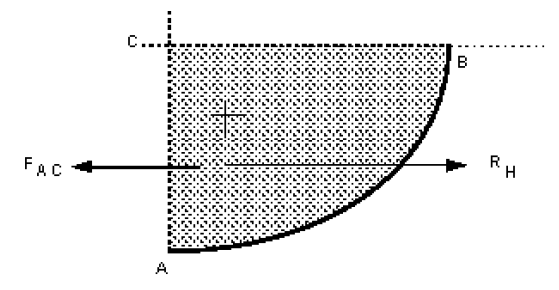
We can see that the horizontal force on AC, , must equal and be in the opposite direction to the resultant force on the curved surface.
As AC is the projection of the curved surface AB onto a vertical plane, we can generalise this to say
The resultant horizontal force of a fluid above a curved surface is:
= Resultant force on the projection of the curved surface onto a vertical plane.
We know that the force on a vertical plane must act horizontally (as it acts normal to the plane) and that must act through the same point. So we can say
acts horizontally through the centre of pressure of the projection of the curved surface onto an vertical plane.
Thus we can use the pressure diagram method to calculate the position and magnitude of the resultant horizontal force on a two dimensional curved surface.
Vertical forces
The diagram below shows the vertical forces which act on the element of fluid above the curved surface.
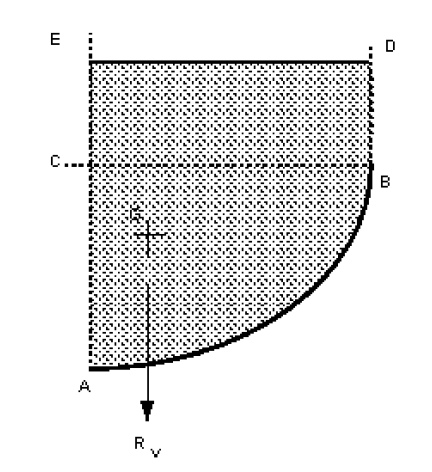
There are no shear force on the vertical edges, so the vertical component can only be due to the weight of the fluid. So we can say
The resultant vertical force of a fluid above a curved surface is:
= Weight of fluid directly above the curved surface.
and it will act vertically downward through the centre of gravity of the mass of fluid.
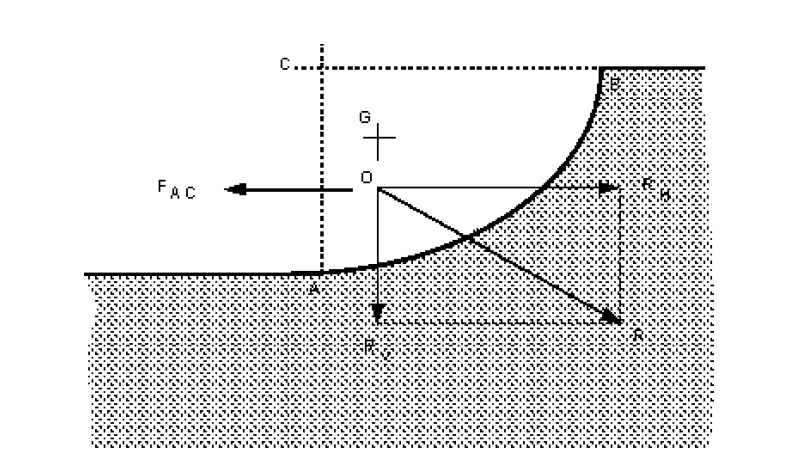
Resultant force
The overall resultant force is found by combining the vertical and horizontal components vectorialy,
Resultant force
And acts through O at an angle of .
The angle the resultant force makes to the horizontal is
The position of O is the point of integration of the horizontal line of action of and the vertical line of action of .
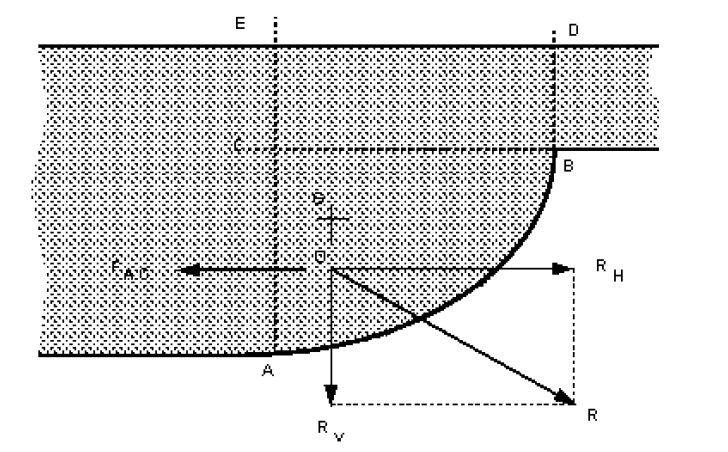
What are the forces if the fluid is below the curved surface? This situation may occur or a curved sluice gate for example. The figure below shows a situation where there is a curved surface which is experiencing fluid pressure from below.
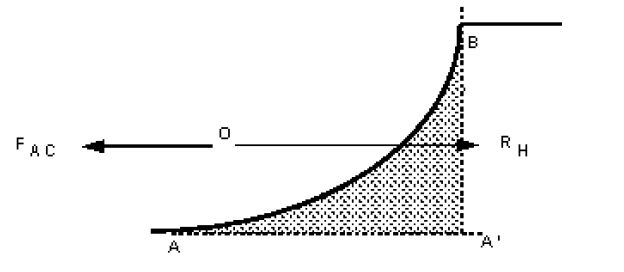
The calculation of the forces acting from the fluid below is very similar to when the fluid is above.
Horizontal force
From the figure below we can see the only two horizontal forces on the area of fluid, which is in equilibrium, are the horizontal reaction force which is equal and in the opposite direction to the pressure force on the vertical plane A’B. The resultant horizontal force, acts as shown in the diagram. Thus we can say:
The resultant horizontal force of a fluid below a curved surface is:
Resultant force on the projection of the
curved surface on a plane
Vertical force
The vertical force are acting are as shown on the figure below. If the curved surface were removed and the area it were replaced by the fluid, the whole system would be in equilibrium. Thus the force required by the curved surface to maintain equilibrium is equal to that force which the fluid above the surface would exert - i.e. the weight of the fluid.
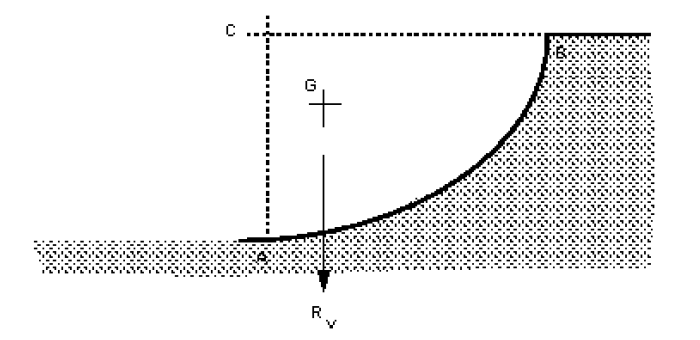
Thus we can say:
The resultant vertical force of a fluid below a curved surface is: Weight of the imaginary volume of fluid vertically above the curved surface.
The resultant force and direction of application are calculated in the same way as for fluids above the surface:
Resultant force
And acts through O at an angle of .
The angle the resultant force makes to the horizontal is