2 Fluids Mechanics and Fluid Properties

What is fluid mechanics? As its name suggests it is the branch of applied mechanics concerned with the statics and dynamics of fluids - both liquids and gases. The analysis of the behaviour of fluids is based on the fundamental laws of mechanics which relate continuity of mass and energy with force and momentum together with the familiar solid mechanics properties.

Objectives of this section

i

Define the nature of a fluid.
ii

Show where fluid mechanics concepts are common with those of solid mechanics and indicate some fundamental areas of difference.
iii

Introduce viscosity and show what are Newtonian and non-Newtonian fluids
iv

Define the appropriate physical properties and show how these allow differentiation between solids and fluids as well as between liquids and gases.

Fluids

There are two aspects of fluid mechanics which make it different to solid mechanics:

i

The nature of a fluid is much different to that of a solid
ii

In fluids we usually deal with continuous streams of fluid without a beginning or end. In solids we only consider individual elements.

We normally recognise three states of matter: solid; liquid and gas. However, liquid and gas are both fluids: in contrast to solids they lack the ability to resist deformation. Because a fluid cannot resist the deformation force, it moves, it flows under the action of the force. Its shape will change continuously as long as the force is applied. A solid can resist a deformation force while at rest, this force may cause some displacement but the solid does not continue to move indefinitely.

The deformation is caused by shearing forces which act tangentially to a surface. Referring to the figure below, we see the force F acting tangentially on a rectangular (solid lined) element ABDC. This is a shearing force and produces the (dashed lined) rhombus element A’B’DC.

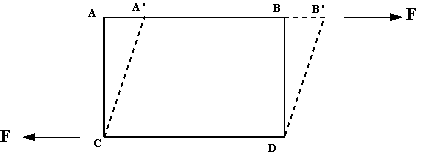
Refer to caption — Figure 1: Shearing force, $F$ , acting on a fluid element.

We can then say: A Fluid is a substance which deforms continuously, or flows, when subjected to shearing forces.

Conversely, this definition implies the very important point that:

If a fluid is at rest there are no shearing forces acting.
i.e. All forces must be perpendicular to the planes which the are acting.

When a fluid is in motion shear stresses are developed if the particles of the fluid move relative to one another. When this happens adjacent particles have different velocities. If fluid velocity is the same at every point then there is no shear stress produced: the particles have zero relative velocity.

Consider the flow in a pipe in which water is flowing. At the pipe wall the velocity of the water will be zero. The velocity will increase as we move toward the centre of the pipe. This change in velocity across the direction of flow is known as velocity profile and shown graphically in the figure below:

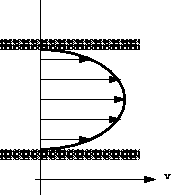
Because particles of fluid next to each other are moving with different velocities there are shear forces in the moving fluid i.e. shear forces are normally present in a moving fluid. On the other hand, if a fluid is a long way from the boundary and all the particles are travelling with the same velocity, the velocity profile would look something like this:

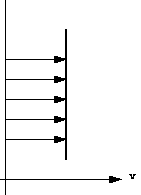
and there will be no shear forces present as all particles have zero relative velocity. In practice we are concerned with flow past solid boundaries; aeroplanes, cars, pipe walls, river channels etc. and shear forces will be present.

2.1 Newton’s Law of Viscosity

How can we make use of these observations? We can start by considering a 3d rectangular element of fluid, like that in the figure below.

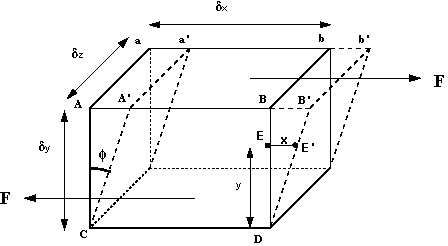
The shearing force $F$ acts on the area on the top of the element. This area is given by $A=\delta s\times\delta x$ . We can thus calculate the shear stress which is equal to force per unit area i.e.

\text{shear stress, }\tau=\frac{F}{A}

The deformation which this shear stress causes is measured by the size of the angle $\phi$ and is know as shear strain.

In a solid shear strain, $\phi$ , is constant for a fixed shear stress $\tau$ .
In a fluid $\phi$ increases for as long as $\tau$ is applied - the fluid flows.

It has been found experimentally that the rate of shear stress (shear stress per unit time, $\tau$ /time) is directly proportional to the shear stress.

If the particle at point $E$ (in figure 4) moves under the shear stress to point $E^{\prime}$ and it takes time $t$ to get there, it has moved the distance $x$ . For small deformations we can write shear strain

	$\displaystyle\text{shear stress, }\tau$	$\displaystyle=\frac{x}{y}$
	$\displaystyle\text{rate of shear stress, }\tau$	$\displaystyle=\frac{\phi}{t}=\frac{x}{ty}=\frac{x}{t}\frac{1}{y}=\frac{u}{y}$

where $\frac{x}{t}=u$ is the velocity of the particle at $E$ .

Using the experimental result that shear stress is proportional to rate of shear strain then

\tau=\text{constant }\times\frac{u}{y}

The term $\frac{u}{y}$ is the change in velocity with $y$ , or the velocity gradient, and may be written in the differential form $\frac{du}{dy}$ . The constant of proportionality is known as the dynamic viscosity, $\mu$ , of the fluid, giving

\tau=\mu\frac{du}{dy}

(1)

This is known as Newton’s Law of Viscosity

2.2 Fluids vs. Solids

In the above we have discussed the differences between the behaviour of solids and fluids under an applied force. Summarising, we have;

1.

For a solid the strain is a function of the applied stress (providing that the elastic limit has not been reached). For a fluid, the rate of strain is proportional to the applied stress.
2.

The strain in a solid is independent of the time over which the force is applied and (if the elastic limit is not reached) the deformation disappears when the force is removed. A fluid continues to flow for as long as the force is applied and will not recover its original form when the force is removed.

It is usually quite simple to classify substances as either solid or liquid. Some substances, however, (e.g. pitch or glass) appear solid under their own weight. Pitch will, although appearing solid at room temperature, deform and spread out over days - rather than the fraction of a second it would take water.

As you will have seen when looking at properties of solids, when the elastic limit is reached they seem to flow. They become plastic. They still do not meet the definition of true fluids as they will only flow after a certain minimum shear stress is attained.

2.3 Newtonian / Non-Newtonian Fluids

Even among fluids which are accepted as fluids there can be wide differences in behaviour under stress. Fluids obeying Newton’s law where the value of ? is constant are known as Newtonian fluids. If $\mu$ is constant the shear stress is linearly dependent on velocity gradient. This is true for most common fluids.

Fluids in which the value of $\mu$ is not constant are known as non-Newtonian fluids. There are several categories of these, and they are outlined briefly below.

These categories are based on the relationship between shear stress and the velocity gradient (rate of shear strain) in the fluid. These relationships can be seen in the graph below for several categories

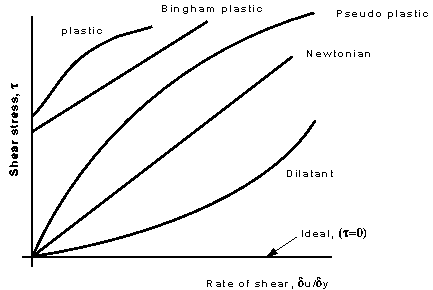
Each of these lines can be represented by the equation

\tau=A+B\left(\frac{\delta u}{\delta y}\right)^{n}

(2)

where $A$ , $B$ and $n$ are constants. For Newtonian fluids $A=0$ , $B=\mu$ and $n=1$ .

Below are brief description of the physical properties of the several categories:

•

Plastic: Shear stress must reach a certain minimum before flow commences.
•

Bingham plastic: As with the plastic above a minimum shear stress must be achieved. With this classification $n=1$ . An example is sewage sludge.
•

Pseudo-plastic: No minimum shear stress necessary and the viscosity decreases with rate of shear, e.g. colloidial substances like clay, milk and cement.
•

Dilatant substances; Viscosity increases with rate of shear e.g. quicksand.
•

Thixotropic substances: Viscosity decreases with length of time shear force is applied e.g. thixotropic jelly paints.
•

Rheopectic substances: Viscosity increases with length of time shear force is applied
•

Viscoelastic materials: Similar to Newtonian but if there is a sudden large change in shear they behave like plastic.

There is also one more - which is not real, it does not exist - known as the ideal fluid. This is a fluid which is assumed to have no viscosity. This is a useful concept when theoretical solutions are being considered - it does help achieve some practically useful solutions.

2.4 Liquids vs. Gasses

Although liquids and gasses behave in much the same way and share many similar characteristics, they also possess distinct characteristics of their own. Specifically

•

A liquid is difficult to compress and often regarded as being incompressible. A gas is easily to compress and usually treated as such - it changes volume with pressure.
•

A given mass of liquid occupies a given volume and will occupy the container it is in and form a free surface (if the container is of a larger volume).
•

A gas has no fixed volume, it changes volume to expand to fill the containing vessel. It will completely fill the vessel so no free surface is formed.

2.5 Causes of Viscosity in Fluids

2.5.1 Viscosity in Gasses

The molecules of gasses are only weakly kept in position by molecular cohesion (as they are so far apart). As adjacent layers move by each other there is a continuous exchange of molecules. Molecules of a slower layer move to faster layers causing a drag, while molecules moving the other way exert an acceleration force. Mathematical considerations of this momentum exchange can lead to Newton law of viscosity.

If temperature of a gas increases the momentum exchange between layers will increase thus increasing viscosity.

Viscosity will also change with pressure - but under normal conditions this change is negligible in gasses.

2.5.2 Viscosity in Liquids

There is some molecular interchange between adjacent layers in liquids - but as the molecules are so much closer than in gasses the cohesive forces hold the molecules in place much more rigidly. This cohesion plays an important roll in the viscosity of liquids.

Increasing the temperature of a fluid reduces the cohesive forces and increases the molecular interchange. Reducing cohesive forces reduces shear stress, while increasing molecular interchange increases shear stress. Because of this complex interrelation the effect of temperature on viscosity has something of the form:

\mu_{T}=\mu_{0}(1+AT+BT)

where $\mu_{T}$ is the viscosity at temperature $T\;^{o}C$ , and is the viscosity at temperature $0\;^{o}C$ . $A$ and $B$ are constants for a particular fluid.

High pressure can also change the viscosity of a liquid. As pressure increases the relative movement of molecules requires more energy hence viscosity increases.

2.6 Properties of Fluids

The properties outlines below are general properties of fluids which are of interest in engineering. The symbol usually used to represent the property is specified together with some typical values in SI units for common fluids. Values under specific conditions (temperature, pressure etc.) can be readily found in many reference books. The dimensions of each unit is also give in the $MLT$ system (see later in the section on dimensional analysis for more details about dimensions.)

2.6.1 Density

The density of a substance is the quantity of matter contained in a unit volume of the substance. It can be expressed in three different ways.

Mass Density

Mass Density, $\rho$ , is defined as the mass of substance per unit volume.

Units: Kilograms per cubic metre, $kg/m^{3}$ (or $kg\;m^{-3}$ )
Dimensions: $ML^{-3}$

Typical values: (at pressure $=1.013\times 10^{-5}Nm^{-2}$ and Temperature $=288.15K$ .)

Water = 1000 $kg/m^{3}$
Mercury = 13546 $kg/m^{3}$
Air = 1.23 $kg/m^{3}$
Paraffin Oil = 800 $kg/m^{3}$ .

Specific Weight

Specific Weight $\omega$ , (sometimes $\gamma$ , and sometimes known as specific gravity) is defined as the weight per unit volume.

The force exerted by gravity, $g$ , upon a unit volume of the substance.

The Relationship between $g$ and $\omega$ can be determined by Newton’s 2nd Law, since

	weight per unit volume	$\displaystyle=\text{mass per unit volume }\times g$
	$\displaystyle\omega$	$\displaystyle=\rho g$

Units: Newton’s per cubic metre, $N/m^{3}$ (or $Nm^{-3}$ )
Dimensions: $ML^{-2}T^{-2}$ .

Water = 9814 $N/m^{3}$
Mercury = 132943 $N/m^{3}$
Air = 12.07 $N/m^{3}$
Paraffin Oil = 7851 $N/m^{3}$ .

Relative Density

Relative Density, $\sigma$ , is defined as the ratio of mass density of a substance to some standard mass density.

For solids and liquids this standard mass density is the maximum mass density for water (which occurs at $4^{o}C$ ) at atmospheric pressure.

Units: None, since a ratio is a pure number.
Dimensions: 1. Typical values: Water = 1, Mercury = 13.5, Paraffin Oil =0.8.

Water = 1
Mercury = 13.5
Air = 0.012
Paraffin Oil = 0.8

2.6.2 Viscosity

Viscosity, $\mu$ , is the property of a fluid, due to cohesion and interaction between molecules, which offers resistance to sheer deformation. Different fluids deform at different rates under the same shear stress. Fluid with a high viscosity such as syrup, deforms more slowly than fluid with a low viscosity such as water.

All fluids are viscous, Newtonian Fluids obey the linear relationship given by Newton’s law of viscosity. $\tau=\mu\frac{du}{dy}$ , which we saw earlier. where $\tau$ is the shear stress,

Units: $Nm^{-2}$ or $kg\;m^{-1}s^{-2}$
Dimensions $ML^{-1}T^{-2}$

$\frac{du}{dy}$ is the velocity gradient or rate of shear strain, and has Units: $s^{-1}$
Dimensions: $T^{-1}$

$\mu$ is the coefficient of dynamic viscosity - see below.

Coefficient of Dynamic Viscosity

The Coefficient of Dynamic Viscosity, $\mu$ , is defined as the shear force, per unit area, (or shear stress $\tau$ ), required to drag one layer of fluid with unit velocity past another layer a unit distance away.

\mu=\tau\bigg{/}\frac{du}{dy}=\frac{\text{Force}}{\text{Area}}\bigg{/}\frac{% \text{Velocity}}{\text{Distance}}=\frac{\text{Force}\times\text{Time}}{Area}=% \frac{\text{Mass}}{\text{Length}\times\text{Area}}

Units: Newton seconds per square metre, $Nsm^{-2}$ or Kilograms per meter per second, $kg\;m^{-1}s^{-1}$ .
(Although note that $\mu$ is often expressed in Poise, $P$ , where $10P=1kg\;m^{-1}s^{-1}$ .)

Typical values:

Water = $1.14\times 10^{-3}\;kg\;m^{-1}s^{-1}$
Mercury = $1.552\;kg\;m^{-1}s^{-1}$
Air = $1.78\times 10^{-5}\;kg\;m^{-1}s^{-1}$
Paraffin Oil = $1.9kg\;m^{-1}s^{-1}$

Kinematic Viscosity

Kinematic Viscosity, $\nu$ , is defined as the ratio of dynamic viscosity to mass density.

\nu=\frac{\mu}{\rho}

Units: square metres per second, $m^{2}s^{-1}$
Although note that $nu$ is often expressed in Stokes, $S_{t}$ , where $10^{4}S_{t}=1m^{2}s^{-1}$ .)
Dimensions: $L^{2}T^{-1}$ .

Typical values:

Water = $1.14\times 10^{-6}kg\;m^{-1}s^{-1}$
Mercury = $1.145\times 10^{-4}\;kg\;m^{-1}s^{-1}$
Air = $1.46\times 10^{-5}\;kg\;m^{-1}s^{-1}$
Paraffin Oil = $2.375\times 10^{-3}\;kg\;m^{-1}s^{-1}$