E4 Questions on Gradually varied flow: Flow Transitions.
-
E4.1
A wide channel consists of two long reaches. The upstream reach has a bed slope of 1 in 100 and the downstream reach has a bed slope of 1 in 1500. The Chezy C for both lengths can be assumed constant and equal to 45. Determine the profile that occurs when the flow per unit width is and determine whether a hydraulic jump occurs and if one occurs which reach of the channel it occurs.
(Answers: , , . Jump in reach 1.)For all flow transition problems you must first calculate the normal depth for reach and the critical depth , for that flow (it will be the same for each reach).
In this example, we have a wide channel which implies that and can be assumed rectangular. This results in , and so .
The Manning’s equation for a wide channel is equation Eq-3
And, applicable to this example, the Chezy equation for a wide channel becomes
Then can be calculated by this explicit expression
For reach 1, and
For reach 2, and
For a wide channel, can be written from equation Eq-17 as
As is the depth when then can be calculated using equation Eq-23:
It is useful to calculate the Froude number of the normal depths as they will be used later. The equation for Fr in a wide channel the Froude number can be calculated from Eq-11:
Which gives and .
We can compare the normal and critical depths for each reach. We see that for reach 1, so the reach is steep and the flow super-critical. Also confirmed as .
For reach 2, so the reach is mild and the flow sub-critical. Also confirmed as .
It is always useful to sketch out the normal and critical depths so that you can start to understand what is physically being calculated and what may be physically possible. These are shown in figure 45.
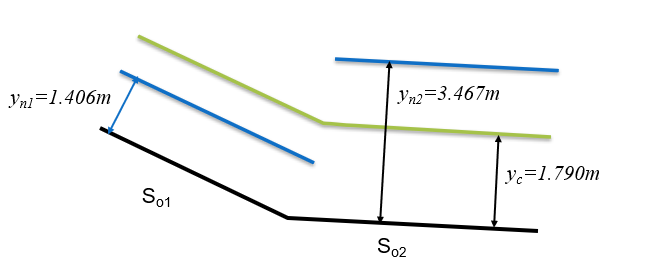
Figure 45: Sketch of slopes and relative critical and normal depths We see that the depths in the two reaches change from below critical depth to above critical depth. The only way that a water surface can join these (and cross critical) is by a hydraulic jump. The hydraulic jump could be in either the upstream reach or the downstream reach, see figure 46. To determine which, we must calculate the conjugate (or sequent) depths for each of the two normal depths.
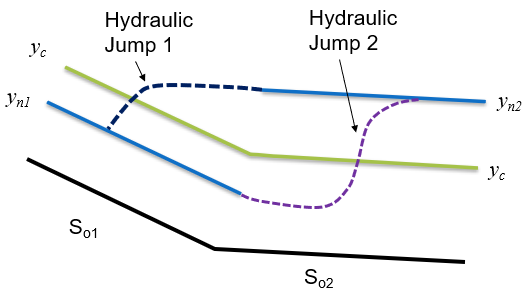
Figure 46: Sketch of possible positions of hydraulic jump joining the two normal depths We calculate the conjugate depth to in reach 1 using the following, where is the conjugate depth in reach 1 using equation Eq-39:
From earlier and , this results in the conjugate depth .
And for the conjugate depth to in reach 2 using the following, where is the conjugate depth in reach 2 using equation Eq-40:
From earlier and , this results in the conjugate depth .
To understand what these two conjugate depths tell us about the position of the hydraulic jump it is again useful to sketch the depths together with the normal and critical depths. This is shown in figure 47
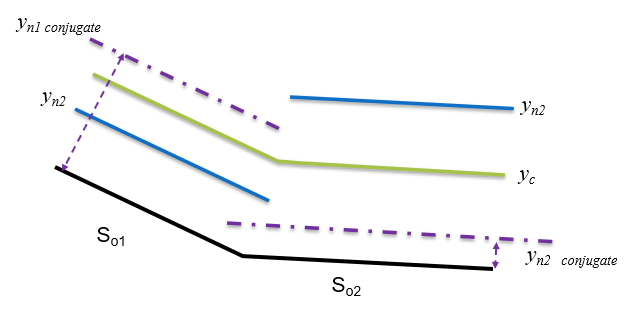
Figure 47: Sketch of conjugate depths in relation to normal and critical depths We can first consider if a jump is possible in reach 1. We see that is greater than the conjugate depth, and above critical, so it could be possible to jump down to that level in reach 1. This is depicted in figure 48. Considering reach 2, we see that the conjugate depth is lower than the normal depth of reach 1. So for a jump to occur the depth would have to drop down to the conjugate, then jump up to . This cannot happen (as there is nothing to cause the drop in level). So the result is a hydraulic jump in reach 1. The surface profile will be an S1. It is in the steep channel and in region 1.
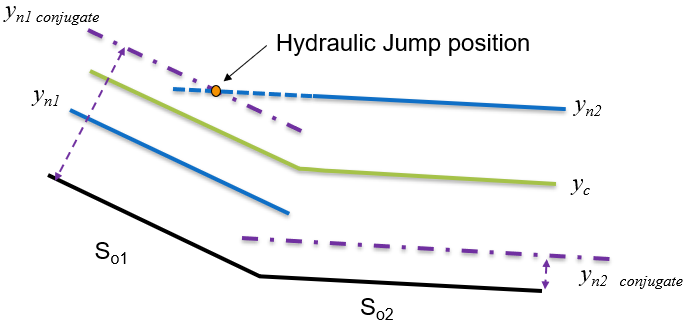
Figure 48: Sketch of conjugate depths and identification of hydraulic jump position -
E4.2
A long wide channel consists of an upstream section with a bed slope of 0.025 and a downstream section with a bed slope of 0.0002. The Chezy C is constant for the whole of the channel and equal to 40 in SI units. When the discharge in the channel is . width demonstrates that a hydraulic jump occurs. Determine in which reach of the channel the jump occurs. Complete your answer with a free-hand sketch of the final profile and label each of the gradually varied profiles.
(Answer: , , , , ) This is very similar to example problem E4.1 so some of the more detailed explanations are not shown here - see that example to see how and why calculations are performed.For all flow transition problems you must first calculate the normal depth for reach and the critical depth , for that flow (it will be the same for each reach). It is also useful to calculate the Froude numbers for each normal depth.
In this example, we have a wide channel and so the Chezy equation for uniform flow in this form is used:
And the can be calculated by this explicitly from equation LABEL: expression
For reach 1, , and , giving For reach 2, is the same at , and , giving
For a wide channel, setting and solving for critical depth gives
It is useful to calculate the Froude number of the normal depths as they will be used later. The equation for in a wide channel is:
Which gives and .
A sketch showing the normal and critical depths helps to understand what is physically being calculated and what may be physically possible. These are shown in figure 49.
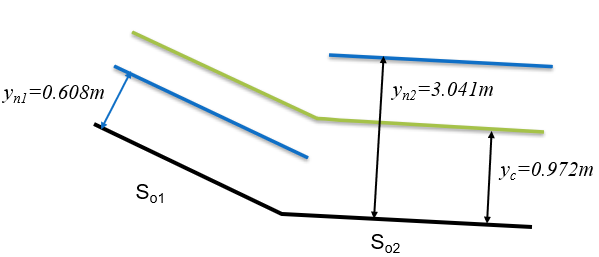
Figure 49: Sketch of slopes and relative critical and normal depths We see that the depths in the two reaches change from below critical depth to above critical depth. The only way that a water surface can join these (and cross critical) is by a hydraulic jump. The hydraulic jump could be in either the upstream reach or the downstream reach, see figure 46 (from the previous example). To determine which, we must calculate the conjugate (or sequent) depths for each of the two normal depths.
We calculate the conjugate depth to in reach 1 from equation Eq-39 to give
and for reach 2, from equation Eq-40 to give
We now need to consider where the hydraulic jump occurs. Considering reach 1, we note that is greater than the conjugate depth, and above critical, so it is possible to jump down to the level in reach 1. This is depicted in figure 50. Considering reach 2, we see that the conjugate depth is lower than the normal depth of reach 1. So for a jump to occur the depth would have to drop down to the conjugate, then jump up to . This cannot happen (as there is nothing to cause the drop in level).
So the result is a hydraulic jump in reach 1. The surface profile will be an S1. It is in the steep channel and in region 1. As shown in figure 50

Figure 50: Sketch of conjugate depths and identification of hydraulic jump position -
E4.3
A wide channel has three reaches each with a different slope. Each can be considered to be long and at the downstream end of the three reaches there is a free outfall. For a specific case, the Chézy C value for all reaches is 32 and the flow per unit width is . The upstream reach has a slope of 1-in-500, the middle reach has a slope of 1-in-50 and the downstream reach has a slope of 1-in-2,000. Determine which flow profile occurs.
(Answer: , , , , , )For all flow transition problems you must first calculate the normal depth for reach and the critical depth , for that flow (it will be the same for each reach). It is also useful to calculate the Froude numbers for each normal depth.
It is a wide channel and we are given a Chezy C so we will use the Chezy equation for uniform flow to calculate normal depths,, equation Eq-7,
And the can be calculated by the explicit equation Eq-10
For reach 1, , and , giving .
For reach 2, is the same at , and , giving .
For reach 3, is still the same at , and , givingFor a wide channel, setting and solving for critical depth gives equation Eq-23
It is useful to calculate the Froude number of the normal depths as they will be used later. The equation for in a wide channel is is equation Eq-18
Which gives , and .
A sketch showing the normal and critical depths helps to understand what is physically being calculated and what may be physically possible. These are shown in figure 51.
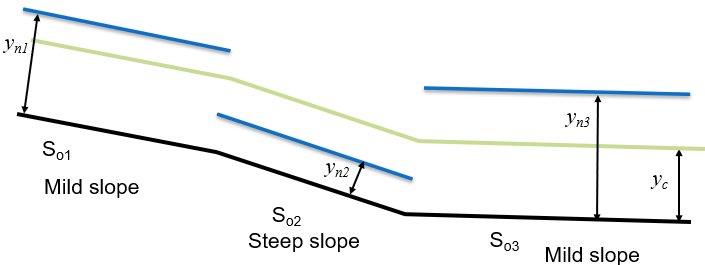
Figure 51: Sketch of slopes and relative critical and normal depths We see that the depths in the three reaches change from above critical depth to below critical depth to above. The slopes are thus mild, steep, mild and at uniform flow would be sub-critical, super-critical, sub-critical respectively.
It is now useful to sketch the possible flow profiles joining the three reaches of uniform flow. Figure 52 shows such a sketch.
Starting from reach 1, we have a normal depth greater than critical which joins to the normal depth lower than critical. To connect these the flow must cross through critical. It does this smoothly at the point where the channel changes slope. This is shown on figure 52 as surface profiles M2 and S2 as profile is in the second region of the mild-sloped reach 1 and the second region of the steep-loped reach 2.
For the change from reach 2 to reach 3 we have to increase depth from below critical to above depth i.e. from sub-critical to super-critical flow. This is only possible via a hydraulic jump. There are two options as show, a jump that occurs in reach 2 or a jump that occurs in reach 3. If it occurs in reach 2, then the surface profile that joins it to will be an S1 (steep-sloped in region 1). If it occurs in reach 3, then the surface profile that joins it to will be an M1 (mild-sloped in region 3).
As the end of the three reaches is a free outfall the flow will be forced to be critical at that outfall, so the depth critical. There will in that case be, at the end of reach 3, an M2 profile as the depth drops from normal, to critical.
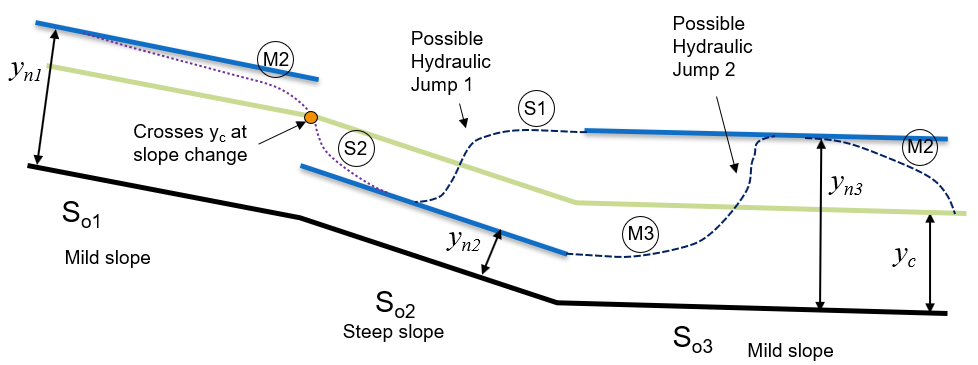
Figure 52: Sketch of possible flow profiles joining the normal depths of the three reaches We now need to consider whether the jump is in reach 2 or reach 3. To determine which, we must calculate the conjugate (or sequent) depths for each of the two normal depths.
We calculate the conjugate depth to in reach 2 from equation Eq-39 to give
and for reach 3 (from equation Eq-40) to give
We now need to consider where the hydraulic jump occurs. Considering reach 2, we note that is greater than the conjugate depth, and above critical, so it is possible to jump down to the level in reach 2. This is depicted in figure 53. Considering reach 3, we see that the conjugate depth is lower than the normal depth of reach 2. So for a jump to occur the depth would have to drop down to the conjugate, then jump up to . This cannot happen (as there is nothing to cause the drop in level).
So the result is a hydraulic jump in reach 2. The surface profile will be an S1. It is in the steep channel and in region 1. As shown in figure 53
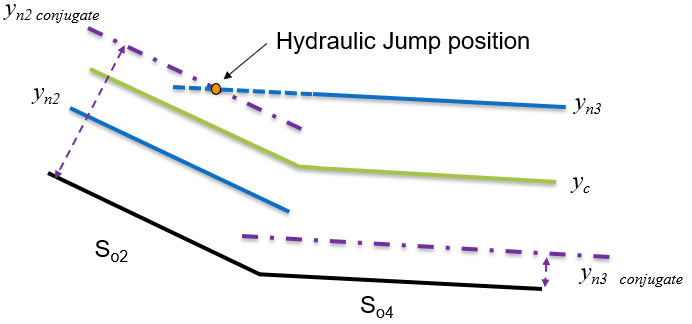
Figure 53: Sketch of conjugate depths and identification of hydraulic jump position for reaches 2 and 3 -
E4.4
A wide channel has two reaches with different bed slopes changing from to . Both reaches have the same cross-section shape and bed roughness of . Sketch the critical flow depth line, uniform flow depth lines, and water surface profile in the channel and identify the type of water surface profile, if the flow discharge per unit width is .
(Answer: , , , M1 profile )This is very similar to example E4.1 and E4.2 but this time uses then Manning’s n to define roughness, so the normal depth calculations will be slightly different.
The Manning’s equation for a wide channel, equation Eq-3 is:
Then can be calculated by this explicit equation Eq-6
For reach 1, and
For reach 2, and
For a wide channel, can be written from equation Eq-17 as
As is the depth when then can be calculated using equation Eq-23:
It is useful to calculate the Froude number of the normal depths as may often be used later. in a wide channel can be calculated from equation Eq-18:
Which gives and .
We can compare the normal and critical depths for each reach. We see that for reach 1, so the reach is mild and the uniform flow sub-critical. Also confirmed as .
Similarly for reach 2, so the reach is also mild and the uniform flow also sub-critical. As again confirmed as .
We can sketch normal and critical depths to help understand the physical situation. This is shown in figure 54

Figure 54: Sketch of normal depth for reach 1 and 2 and the critical depth We need to decide which profile joins the two normal depths. They are both mild so it will be an M profile. One option would be for the depth to rise in reach 3 with an M2 profile. However, an M2 falls in the direction of flow and we need it to rise. So the only option is for an M1 profile in reach 1 which rises asymptotically from to , again joining the normal depth asymptotically. This is sketched in figure 55
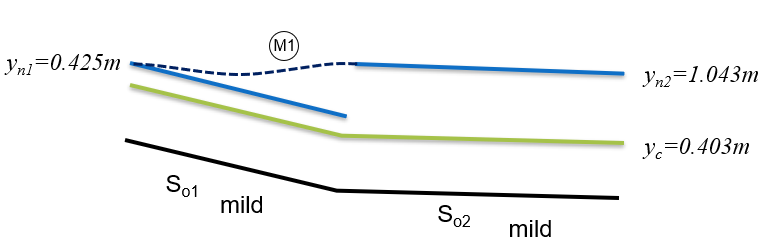
Figure 55: Sketch of the M1 water surface profile connecting the normal depths of reach 1 and reash 2 -
E4.5
A wide channel consists of three long reaches. The upstream reach has a bed slope of 1 in 500, the middle reach a slope of 1 in 50, and the downstream reach slope of 1 in 1,750. The Chezy C for all three lengths can be assumed constant and equal to 27. Determine the profiles that occur if the flow per unit width is .
(Answer: , , , , , . Jump in reach 2 (middle). )For all flow transition problems you must first calculate the normal depth for reach and the critical depth , for that flow (it will be the same for each reach). It is also useful to calculate the Froude numbers for each normal depth.
It is a wide channel and we are given a Chezy C so we will use the Chezy equation for uniform flow to calculate normal depths, equation Eq-7
And the can be calculated by this explicit equation Eq-10
For reach 1, , and , giving .
For reach 2, is the same at , and , giving .
For reach 3, is still the same at , and , givingFor a wide channel, setting and solving for critical depth gives equation Eq-23
It is useful to calculate the Froude number of the normal depths as they will be used later. in a wide channel is given by equation Eq-18:
Which gives , and .
A sketch showing the normal and critical depths helps to understand what is physically being calculated and what may be physically possible. These are shown in figure 56.
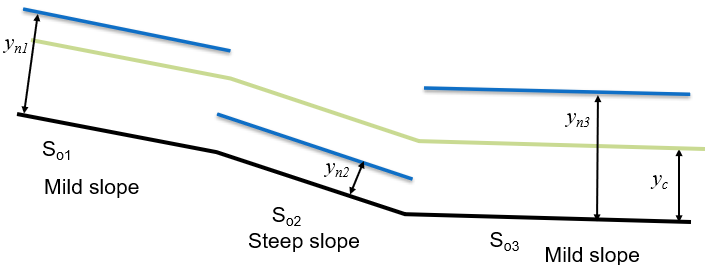
Figure 56: Sketch of slopes and relative critical and normal depths We see that the depths in the three reaches change from above critical depth to below critical depth to above. The slopes are thus mild, steep, mild and uniform flow would be sub-critical, super-critical, sub-critical.
It is now useful to consider and sketch the possible flow profiles joining the three reaches of uniform flow. Figure 57 shows such a sketch.
Starting from reach 1, we have a normal depth greater than critical which joins to the normal depth lower than critical. To connect these the flow must cross through critical. It does this smoothly at the point where the channel changes slope. This is shown on figure 57 as surface profiles M2 and S2 as the profile is in the second region of the mild-sloped reach 1 and the second region of the steep-loped reach 2.
For the change from reach 2 to reach 3 we have to increase depth from below critical to above depth i.e. from sub-critical to super-critical flow. This is only possible via a hydraulic jump. There are two options as shown, a jump that occurs in reach 2 or a jump that occurs in reach 3. If it occurs in reach 2, then the surface profile that joins it to will be an S1 (steep-sloped in region 1). If it occurs in reach 3, then the surface profile that joins it to will be an M1 (mild-sloped in region 3).
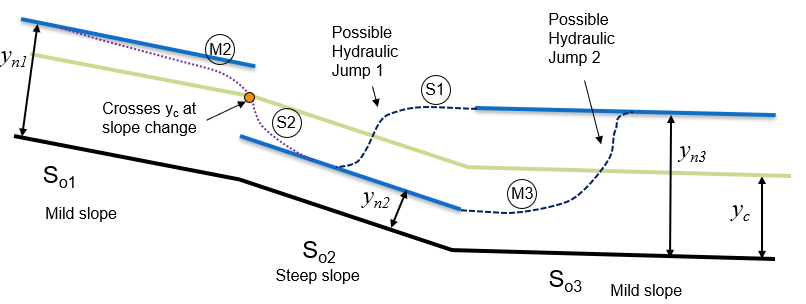
Figure 57: Sketch of possible flow profiles joining the normal depths of the three reaches We now need to consider whether the jump is in reach 2 or reach 3. To determine which, we must calculate the conjugate (or sequent) depths for each of the two normal depths.
We calculate the conjugate depth to in reach 2 from equation Eq-39 to give
and for reach 3 (from equation Eq-40) to give
We now need to consider where the hydraulic jump occurs. Considering reach 2, we note that is greater than the conjugate depth, and above critical, so it is possible to jump down to the level in reach 2. This is depicted in figure 58. Considering reach 3, we see that the conjugate depth is lower than the normal depth of reach 2. So for a jump to occur the depth would have to drop down to the conjugate, then jump up to . This cannot happen (as there is nothing to cause the drop in level).
So the result is a hydraulic jump in reach 2. The surface profile will be an S1. It is in the steep channel and in region 1. As shown in figure 58
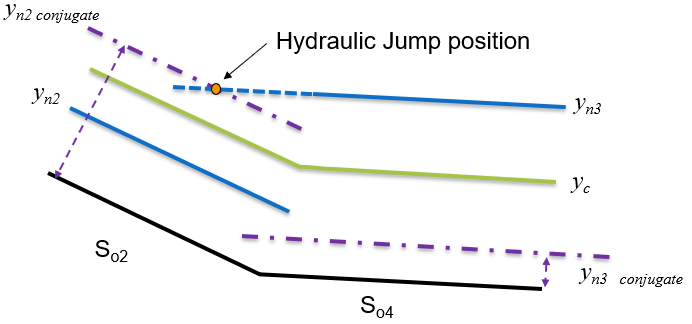
Figure 58: Sketch of conjugate depths and identification of hydraulic jump position for reaches 2 and 3