E2 Questions on Rapidly Varied Flow - Sudden transitions and Hydraulic Jumps
-
E2.1
For a trapezoidal channel with a , and side slope 1 vertical 2 horizontal, calculate the critical depth if the discharge is .
(Answer: )The question asks for the critical depth, that is the depth when Froude number .
We have for the Froude number this general equation Eq-11
Written in terms of gives Eq-12:
And at critical flow, when the depth is critical, then
Or, more conveniently for calculation
We are considering the trapezoidal channel as shown in figure 17, the area of flow section and the wetted perimeter are given as
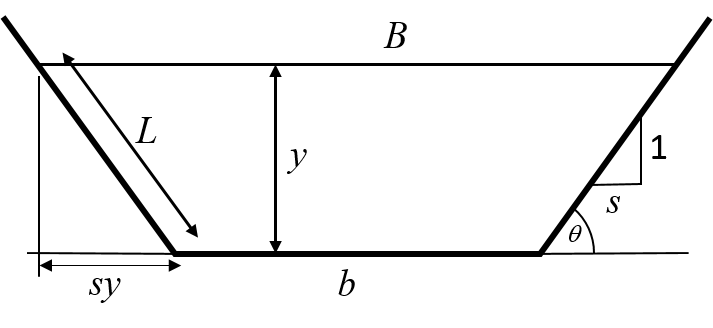
Figure 17: A trapezoidal channel section This can be written in terms of critical depth, :
To solve for (given and ) requires an iterative solution method. The iteration table shown in figure 18 solves this using the secant method. The solution is .
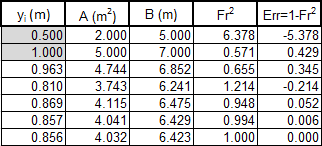
Figure 18: Iteration table calculating for a trapezoidal channel -
E2.2
Water is flowing at a normal depth in a wide rectangular channel with a bed slope of 1:500. If Manning’s and the discharge is . Calculate the height of a bump that would produce the critical flow without causing backwater upstream (i.e. without raising the upstream water level). (Answer: , Bump height )
First of all Manning’s equation needs to be solved for normal depth in the rectangular channel. An iteration table can be set up to do this. The table of figure 19 demonstrates this, and a solution of is calculated.
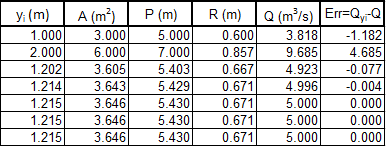
Figure 19: Iteration table calculating for a rectangular channel If we consider the flow over a bump. The depth at point 1, just upstream of the bump, will be .

Figure 20: Steady flow over a raised bump We can apply the specific energy concept from point 1 to point 2, just on the bump.
or
or
, critical depth. We can write the Froude number squared, at critical depth in a rectangular channel, from Eq-14 as
so, using
giving
Applying , with in the specific energy equation we get .
-
E2.3
Water is flowing at a velocity of and a depth of in a channel of rectangular section with a width of . Find the changes in depth produced by
-
(a)
A smooth contraction to a width of 3.0m
-
(b)
The smallest allowable contraction for the flow to be possible upstream as described.
(Answer: (a) , (b) )
We have and thus .
Apply the specific energy equation from point 1 just upstream to point 2 in the throat.
or
or
or using flow per unit width, and , then
or
Part E2.3a: Solve the above for given . We have the cubic
We can calculate so the cubic equation to solve becomes
This must be solved using a numerical tool or trial and error to give these 3 solutions .
We know the negative solution is not physically possible, so can discount that. We need to check whether the approach flow is sub or super-critical. We need to calculate the critical depth upstream
Also, we need to calculate the critical depth in the contraction
The critical depth in the contraction cannot be passed so as the upstream flow is subcritical as , and depth will drop from to (it cannot physically pass and drop down to .
We can see this on the specific energy curves and depths shown in figure 21. The solid horizontal green line intersects with the blue , curve at , . The vertical dark blue line drawn down from that point intersects the orange , curve at .
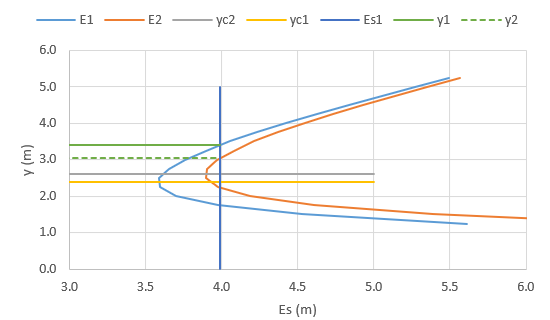
Figure 21: Specific Energy curves , , and depths , and , Part E2.3b: The upstream flow depth will not be affected by the contraction width unless it goes narrower than the critical width, i.e. the width when the depth in the contraction is critical. We know that (or ) can be expressed in terms of as Eq-33
And as and because of conservation of energy this gives
Using the expression for at critical depth we can calculate the minimum width to not affect the upstream depth
-
(a)
-
E2.4
The normal depth of flow in a rectangular channel (with a 5m wide bases and 2m high side walls) is 1m. It is laid to a slope of 1m/km with Manning’s . Some distance downstream there is a hump of height 0.5m on the stream bed. If critical flow occurs on the bump, determine the depth of flow () immediately upstream of the bump and the depth of flow () above the bump. If the bump is reduced to 0.1m, what values will and be?
(Answer: , , , , )We first calculate the flow in the channel using Manning’s equation for a rectangular channel given, , , and
Apply the specific energy equation from point 1 just upstream to point 2 above the bump with representing the height of the bump.
or
or (and considering that )
or using flow per unit width, , then
First, we need to know whether the flow arriving at the bump is sub or super-critical. To do this calculate the Froude number, Eq-13:
So the flow is sub-critical.
We could have calculated the critical depth Eq-22:
And as this is less than the normal depth this confirms that flow is sub-critical.
We have two possibilities here: 1) that the bump is less than the critical height, will stay the same and will drop over the bump so we need to calculate , or 2) the bump is greater than the critical height and so depth over the bump will be critical and the depth will increase upstream, so we need to calculate . (of course, if the bump is equal to critical height, then would not change.)
So, we need to calculate the critical bump height. If we set and use the other given values then we have
As (or ) and
As the bump height, is greater than this , then and we need solve for
Which, using the known values, gives
This can be solved using a numerical tool or trial and error to give these 3 solution values .
We know that the depth upstream must increase (from ), so the solution is , and
If the bump height is , then as this is less than the critical bump height (of ), the depth upstream will not change from the normal depth (of ), but the depth over the bump will fall.
We simply take the same specific energy equation as above and now solve for using and .
Which, using the known values, gives
This can be solved using a numerical tool or trial and error to give these 3 solution values .
We know that the depth must drop from and that the depth cannot be less than , and as the negative depth is not physically possible, the solution is .
-
E2.5
Water is flowing at a rate of through a rectangular channel wide, at a depth of . A weir downstream causes the water to back up the channel and a hydraulic jump occurs. Find the sequent depth and the loss of energy at the jump.
(Answer: , )We will use the following equation that relates depths on each side of a hydraulic jump, Eq-39:
First calculate the velocity and Froude numbers using , ,
Froude number for the rectangular channel
It is useful to calculate the specific energy of the flow, as we need to calculate how much is lost in the jump, so
Applying the hydraulic jump equation gives the height of the jump (the sequent depth):
Then and
So loss of energy in the jump is
Alternatively, this formula can be used to calculate the energy loss in a jump
-
E2.6
Water flows in a rectangular channel at a depth of 30cm and with a velocity of . If a downstream sill forces a hydraulic jump, what will be the depth and velocity downstream of the jump? What head loss is produced by the jump?
(Answer: , , )This is very similar to the previous question, however this time we do not know the width, so we work with flow per unit width, .
We will again use the following equation that relates depths on each side of a hydraulic jump:
First calculate the flow per unit width () and Froude numbers using ,
Froude number for the rectangular channel Eq-11
Calculate the specific energy of the flow, LABEL:eqn:specific_energy
Applying the hydraulic jump equation gives the height of the jump (the sequent depth):
Then and
So loss of energy in the jump is
Alternatively, the formula Eq-41 can be used to calculate the energy loss in a jump
-
E2.7
Water passes under a sluice gate in a horizontal channel of width 2m. The depths of flow on either side of the sluice gate are and . A hydraulic jump occurs a short distance downstream. Assuming no energy loss at the gate, calculate:
-
(a)
The force on the gate
-
(b)
The depth of flow downstream of the hydraulic jump
-
(c)
The fraction of the fluid energy that is dissipated in the jump
(Answer: , , Fraction of energy lost (dissipated) )
We will consider the arrangement and labelling shown in figure 22 for the depths in all subsequent equations.
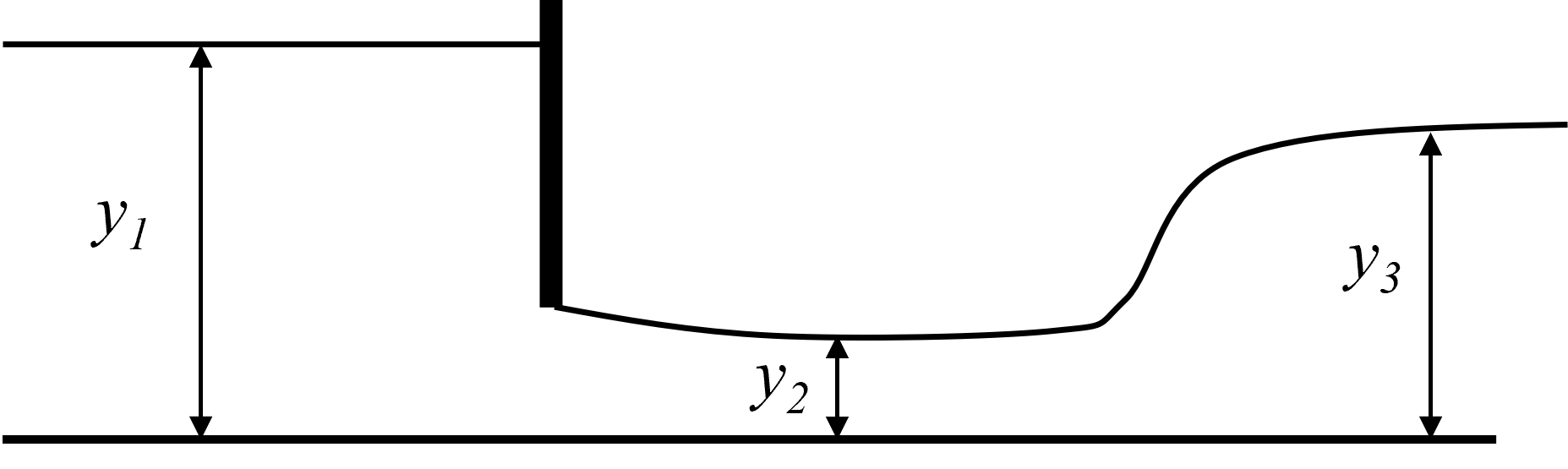
Figure 22: Sluice and hydraulic jump arrangements We first need to determine the flow rate using the given depths, and . This can be done using the specific energy equation. In terms of flow per unit width, this can be written as equation Eq-32:
This can be rearranged in terms of :
And applying the known depths
and thus (or )
We can now calculate the velocities:
and
For E2.7a to find the force on the gate we need to apply the force equation
Where, is the force on the gate, and is the total force (force due to the rate of change in momentum), given by:
or in terms of flow per unit width
And is the pressure force (force due to changes in pressure), given by:
For a rectangular channel, where and , so
Putting these together gives
so
Or, force on the gate .
For E2.7b we know that the hydraulic jump occurs soon after the gate, so we can assume the conditions from the above calculation: i.e. just upstream of the jump, depth, and velocity, .
And the Froude number here is equation Eq-16
We will apply the hydraulic jump equation as previously, using the upstream location as and the downstream as , following the notation in figure 22 The hydraulic jump equation Eq-39 is thus
For E2.7c we need to calculate the specific energy on both sides of the jump.
Velocity downstream of the jump is calculated as
So
So loss of energy in the jump is
The fraction of energy loss is
Which in percentage terms is an energy loss of .
-
(a)