E1 Questions on Uniform Flow and Critical Flow. - Calculation of normal and critical depth.
-
E1.1
A rectangular channel is wide, has a 0.01 slope, flow rate of , and . Find its normal depth and critical depth .
(Answer: , )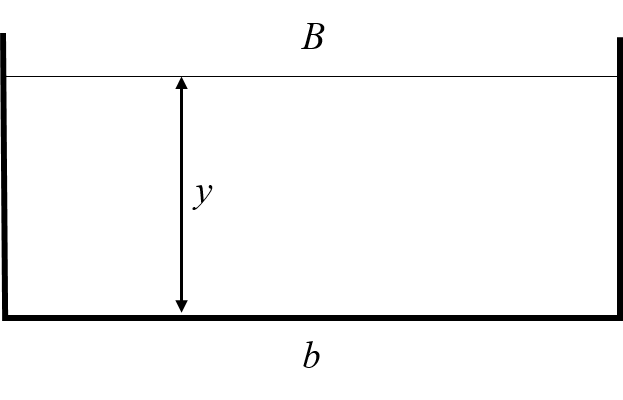
Figure 1: A rectangular channel section For a rectangular channel, we have:
and
so
The Chezy equation, eqn Eq-1, for a rectangular channel (writing as we are now using a uniform flow equation) becomes:
(1)The Manning equation, eqn Eq-2, for a rectangular channel becomes:
(2)This equation must be solved for by a suitable numerical solution (e.g. trial and error or secant method). This gives:
At critical depth , , so using equation Eq-13:
And also then
For a rectangular channel this simplifies (using ) to
This can be formulated to be solved explicitly for :
To give
You could also note that this can be formulated using the unit flow concept , so Which again can be simplified to
Then as ,
-
E1.2
Water flows in a long rectangular channel at a depth of and discharge of . Determine the minimum channel width if the channel is to be sub-critical.
(Answer: )The maximum depth will give the minimum width for a given flow. As the channel is to flow sub-critical then the critical depth is the limiting maximum depth. We have then and and can use at critical depth. Equation Eq-13 gives:
Which gives
-
E1.3
A rectangular channel has a bottom width of and Manning’s
-
(a)
Determine the slope to give a normal depth of when the discharge is
-
(b)
Determine the critical slope and the critical depth when the discharge is
-
(c)
Determine the critical slope to give a the critical depth of 1.5m and compute the corresponding discharge.
(Answer:(a) , (b) , , (c) , )
(a) Using Manning’s equation and the formulae for a rectangular channel in terms of , iterate to solve for slope
We have , and Manning’s .
Iterating gives the solution or 1 in 4167.
(b) Critical slope is the slope when the normal depth, , is equal to the critical depth
Critical Slope, , can be calculated by rearranging Manning’s equation and substituting in the geometric parameters calculated at critical depth i.e.
and
leading to
This results in and , and thus or 1 in 115
Alternatively, the formula for critical slope, Eq-24, could be used directly.
(3)(where for a rectangular channel)
(c) For this part we must calculate a new value of that will give critical depth , so using equation Eq-22
Which give
Using we get and , and, as above, we can cacluate or 1 in 122
-
(a)
-
E1.4
For a trapezoidal channel with a base width , Manning’s and side slope (i.e. 1 vertical: 2 horizontal), calculate the critical depth, critical velocity, and critical slope if its discharge .
(Answer:, s, )For any channel, the critical depth can be found by solving equation Eq-14 equated to 1.
For a trapezoidal channel, we have:
and
and
Substitution for and and iterating for gives the solution
Velocity in any channel is
Substituting, to give and using , gives .
The formula for critical slope, Eq-24, could be used directly.
(4)From the data, , , , and this gives or 1 in 129
-
E1.5
A rectangular channel wide carries of water when flowing deep. Work out the flow’s specific energy. Is the flow sub-critical or super-critical?
(Answer: m and flow is sub-critical)Specific Energy is given by Eq-27,
(5)Taking, as usual, then
(6)Calculate the Froude number to determine is sub or super-critical flow. For a rectangular channel Eq-16 gives
, so flow is sub-critical.
Alternatively, we could calculate the critical depth and compare this to the current depth. For a rectangular channel critical depth is given by Eq-22
As , i.e. the depth of flow is greater than the critical depth, the flow is sub-critical.
-
E1.6
Two engineers observed two rivers and recorded the following flow parameters: River 1: flow discharge , flow velocity , water surface width ; River 2: flow discharge , flow velocity , water surface width . Decide the flow regime of two rivers, i.e. sub-critical or super-critical.
(Answer: River 1 is sub-critical and River 2 is super-critical)For any channel, the Froude number (squared) can be found from either Eq-20
or in terms of velocity
We can calculate from .
For River 1: , , so and as then
For River 2: , , so and as then
So River 1 is flowing sub-critical, River 2 is flowing super-critical.
-
E1.7
A concrete, trapezoidal channel has a bottom slope of and a Manning roughness factor of . The bottom width of the channel is , and the side slopes are 1 in 2. Determine the velocity and discharge when the flow is normal at a depth of .
(Answer: , )The solution is a straightforward use of Manning’s equation Eq-2 applied for a trapezoidal channel.
So
And the velocity of flow in the channel is
-
E1.8
A trapezoidal channel has a bottom slope of in and a Manning roughness factor of . The bottom width of the channel is , and the side slopes are 1 in 3. Determine the normal depth in this channel for .
(Answer: ). For a rectangular channel, we have:and
so
Manning’s equation Eq-2 is
We have , Manning’s , and .
Iterating gives the solution .
-
E1.9
The discharge in uniform flow in a rectangular channel wide is when the slope is 1:100. Is the flow sub-critical or super-critical? Calculate the slope, , that would give critical depth. The Manning roughness coefficient is .
(Answer: super-critical, , ).Iterate the Manning’s equation to solve for to give .
Then and
Critical depth for a rectangular channel can be calculated from or , leading to Eq-22
From the Manning’s equation is found
, , and thus or 1 in 440
Compound Channels
-
E1.10
The cross-section of a stream can be approximated by the compound channel shown in figure 2. The bottom slope is . The Manning roughness factor for the main channel and for the overbank areas. Determine the normal depth for a discharge of . Also, calculate the energy coefficient and the momentum coefficient for the channel with this flow condition.
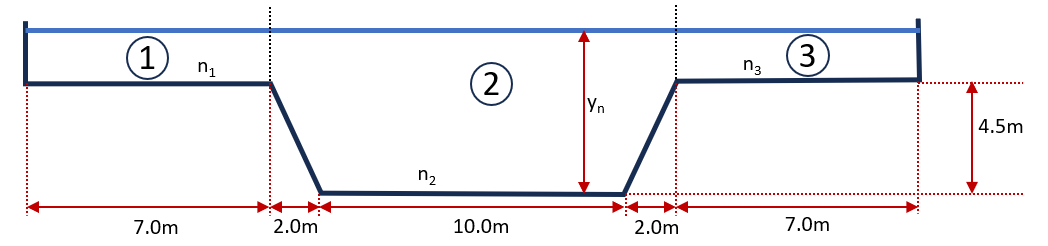
Figure 2: A Compound section (Answer: , , .)
We will apply Manning’s equation for each of the three regions and the total flow will be the sum of the three calculated flows.
We will need to perform an iterative solution to solve Manning’s equation for . If we assume that the normal depth is such that flow is in the flood plains, and our depth is , then we have, from the geometry in figure 3, depth on the flood plain as
and
where
And also
where
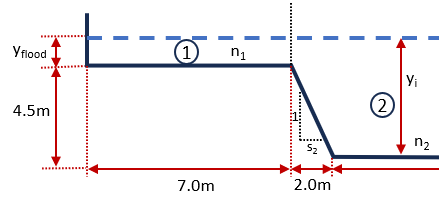
Figure 3: Section detail for given , , , and can calculate the side slope from the section geometry as
An iteration table can be set up in, say, Excel and each of the above geometric and physical parameters calculated for a given . Then for each of the three regions, and then the total can be calculated and compared against the target of . The first iteration is shown in figure 4, for an initial , equivalent to

Figure 4: Iteration table headings and initial calculation with The aim of the iteration is to reduce the error to be small . This can be done by various methods including trial and error. Here we will use the secant method to estimate the solution. The secant method uses the following formula, where in the table of figure 4.
(7)For the second we have taken , so that . And applying the secant method we get the result shown in he table of figure 5 with .
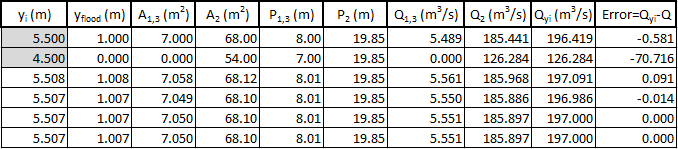
Figure 5: Complete iteration table -
E1.11
The total width of the channel considered in Question E1.10 is to be decreased by reducing the overbank portions symmetrically; however, this reduction must not cause an increase of more than in the flow depth for the discharge of . Assuming normal depth still is present in the channel, determine the minimum allowable channel total width, .
(Answer: .)The solution to this question requires finding a width such that is the normal depth from E1.10, , plus i.e. . We can perform an iteration similar to that in E1.10 (calculating , , and ) for an estimated , and the target of the iteration will be the same , so the error function will be .
For a given we must calculate the floodplain width
So the formulae that change from question E1.10 are those for . As we know that then
and
The table of figure 6 shows this implemented in a similar way to that of question E1.10 with estimated via a secant method and taking (full flood plain), and (no flood plain) as initial values. This shows the solution of , or the width of each flood plain being .
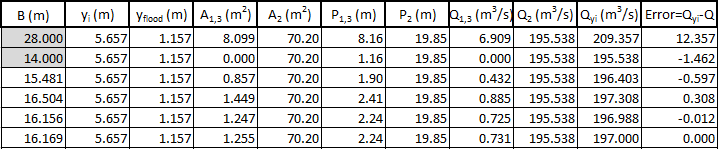
Figure 6: Complete iteration table for -
E1.12
The cross-section of a river with flood plains flowing in uniform flow may be idealized as shown in Fig. 7. Determine the discharge carried by the river when its dimensions and roughness parameters are:
Bed slope:
Manning’s ns:
Side slopes:
Bed widths: , ,
Main channel depth:and
Normal depth
(Answer: .)
Figure 7: Idealized river channel with flood plains The equations for each geometry element can be written as functions of the depth where also
is calculated from Manning’s equation for each of the regions
And so .
Implementing these formulae in a tabular form results in the table of figure 8, which shows .

Figure 8: Table calculating for give As an extra exercise, the table could be set up to iterate to find a normal depth given a flow . As a test, if the target is set to , the solution from an iteration should give . Such an iteration has been performed using the secant method and is shown in figure 9. With initial estimates of and this iterates to in 4 further iterations.

Figure 9: Iteration table for where Using this iteration table, we could answer the question, what is the normal depth for different flows? E.g. the table of figure 10, shows that the solution for a flow of is a normal depth

Figure 10: Iteration table for where -
E1.13
For the channel of question E1.12 calculate the flow, if all dimensions, including the normal depth were the same, but the slope of the channel is 0.002.
(Answer ).This follows the calculation of geometry of question E1.12, with the calculations for changed to take account of . If the table has been set up appropriately in the spreadsheet then a simple change of the value will give a solution of , and the table shown in figure 11

Figure 11: Table calculating for Efficient Channels
-
E1.14
A trapezoidal channel has side slopes of 1:3/4 and the slope of the bed is 1 in 2000. Determine the optimum dimensions of the channel if it is to carry water at . Use the Chezy formula, assuming that .
(Answer: , ).Let us review the concept and equations for efficient channels. We would want to minimise the excavation and materials used to construct the channel. This suggests that the designed channel should have a maximum hydraulic radius for a given area or minimum perimeter for the given area since hydraulic radius . A semi-circular channel would be the most optimal. However, we must consider channel shapes that are to be built.
In this example, we will consider a trapezoidal channel section, as shown in figure 12,
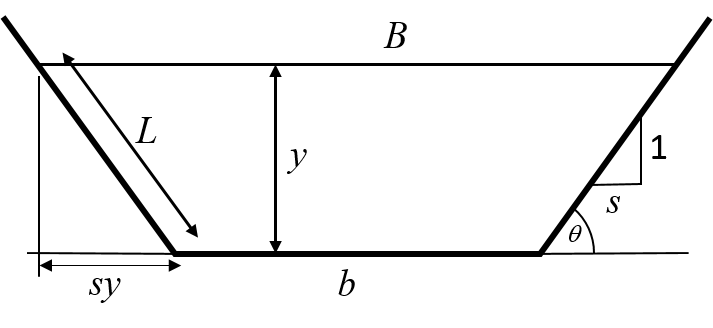
Figure 12: A trapezoidal channel section the area of flow and the wetted perimeter are given by these familiar equations
(11)(12)Rearranging the equation for to give , then substituting this into equation 12 for gives
(13)To minimize , evaluate with and constant and set equal to zero. Therefore,
and rearranging we can obtain an expression for the area to give this optimum :
(14)Substituting the expression for into Eq. 11, one gets
(15)Likewise, substituting the value of from Eq. 14 in Eq. 13, one gets
or
(16)Thus, for a minumum wetted perimeter ,
(17)Equation 17 indicates that for a trapezoidal section channel and for any side slope (or ), the most efficient uniform flow channel would be the one for which the hydraulic radius is half the depth of flow.
So the Manning’s equation Eq-2 for uniform flow in the most efficient trapezoidal section channel would be
And for the Chezy equation Eq-1
So we have an equation (either Manning’s or Chezy) that has two unknowns, and . But we know a relationship between and from equation 15. And using
So the Chezy equation for this channel section becomes
This can be solved iteratively with a target of and . The table of figure 13 shows this iteration using the secant method and that the solution is and
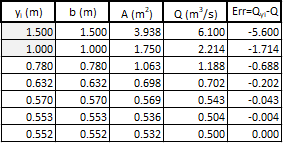
Figure 13: Iteration table calculating for efficient trapezoidal channel , and target -
E1.15
An open channel with is to be designed to carry of water at a slope of 0.0065. Find the most efficient cross-section for a rectangular section.
(Answer: ).See question solution E1.14 for the following equations for efficient trapezoidal channels. The equation of the only variable we can change in this question is that for the bed width, , equation 15
For a square channel the . Using this with the familiar equations for the geometry of a trapezoidal channel
and
and with the usual form of the Manning’s equation
then an iteration can be performed to solve for and thus .
The table of figure 14 shows this iteration using the secant method and that the solution is and
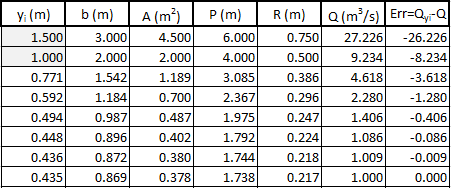
Figure 14: Iteration table calculating for efficient rectangular channel , and target -
E1.16
A rectangular channel has width and normal depth . What is the diameter of a semicircular channel that will have the same discharge as in the rectangular channel, when flowing just full in uniform flow? Assume that and are the same in the two cases. Compare the two wetted perimeters.
(Answer: , ,For this, we need to first calculate the for the rectangular channel for the given parameters using Manning’s equation Eq-2
Then second, apply the manning equation for a circular channel and equate the . When the channel (pipe) is just full, ie. depth is equal to the diameter or we should realise that the area, , will be the area of the circle and the wetted perimeter, , the circumference of the same circle. i.e.
So
The Manning’s equation can then be written for a ’just-full’ pipe as
Equating this with the Manning’s equation for a rectangular channel gives:
As and are the same for both channels these terms can be cancelled to give
And rearranged to give :
Which results in .
Comparing the wetted perimeters we can simply calculate these as
, . -
E1.17
What are the dimensions of the most efficient rectangular channel section to carry at a slope of 1 in 900. The surface of the channel is of concrete.
(Answer: , using )From the earlier section on Efficient uniform flow channels we saw that for a trapezoidal channel, the most efficient section is when
and
For a rectangular channel then and so
So Manning’s equation Eq-2 becomes, for an efficient rectangular channel
This requires an iterative solution. A table showing this solved using the secant method is shown in figure 15. The result is that and
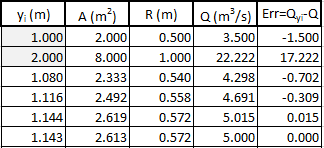
Figure 15: Iteration table calculating for an efficient, concrete-lined, rectangular channel -
E1.18
What is the most efficient depth for a brick channel of a trapezoidal section with sides sloping at to the horizontal to carry . The bed slope is 0.0009.
(Answer: , using )This requires an iterative solution. A table showing this solved using the secant method is shown in figure 16. The result is that using for the brick lining.
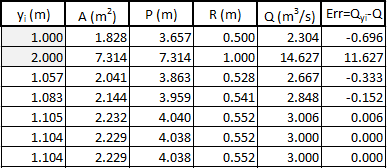
Figure 16: Iteration table calculating for an efficient trapezoidal, brick-lined channel