E3 Questions on Gradually varied flow - including integration of the backwater curve.
-
E3.1
A Rectangular channel is 3.0m wide, has a 0.01 slope, discharge of , and n=0.011. Find and . If the actual depth of flow is 1.7m, what type of profile exists?
(Answer: = 0.4m, = 0.683m, S1 Curve) -
E3.2
A rectangular channel with a bottom width of and a bottom slope of has a discharge of . In a gradually varied flow in this channel, the depth at a certain location is found to be assuming , determining the type of GVF profile, the critical depth, and the normal depth.
(Answer: M2, , ) -
E3.3
The figure below shows a backwater curve in a long rectangular channel. Determine using a numerical integration method, the profile for the following high flow conditions: , , , and a bed slope of . Take the depth just upstream of the dam as the control point equal to . At what distance is the water level not affected by the dam? perform your integration using a) 2-steps and b) 10-steps
(Answer: .
Using (Euler) 2-step , 10-step .
Using 2-step , 10-step .
Using a forth-order Runge Kutta method gave 2-step , 10-step ) -
E3.4
A trapezoidal, concrete-lined, channel has a constant bed slope of , a bed width of , and side slopes of . A control gate increased the depth immediately upstream to . When the discharge is compute the water surface profile upstream and identify the distance when the water depth is . ()
(Answer: Using (Euler) 2-step , 10-step .
Using 2-step , 10-step .
Using mean GVF function: 2-step , 10-step .
Using a forth-order Runge Kutta method gave 2-step , 10-step ) -
E3.5
Using the figure below, determine the profile for the channel conditions using a step length of . , , the bed slope of the rectangular channel is and has a width of . The sill height of the weir is and the water depth over the weir is . Compare results from each method.
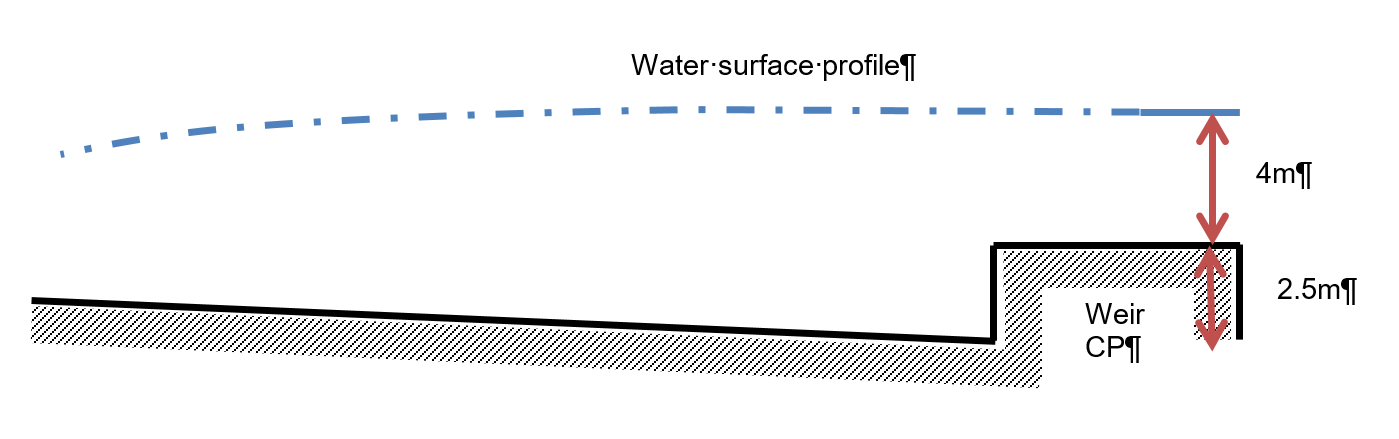
Figure 4: The backwater curve for question E3.5