E1 Questions on Uniform Flow and Critical Flow. - Calculation of normal and critical depth.
-
E1.1
A rectangular channel is wide, has a 0.01 slope, flow rate of , and . Find its normal depth and critical depth .
(Answer: , )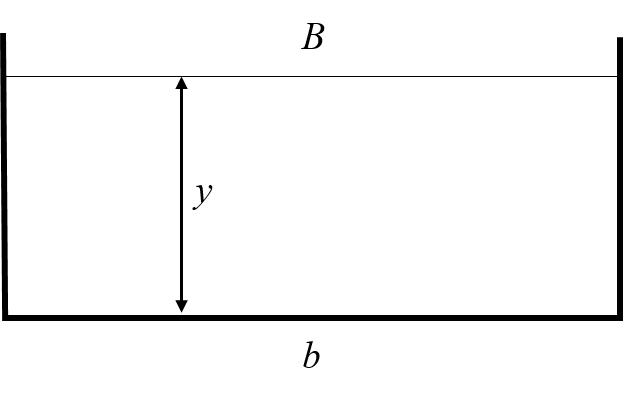
Figure 1: A rectangular channel section -
E1.2
Water flows in a long rectangular channel at a depth of and discharge of . Determine the minimum channel width if the channel is to be subcritical.
(Answer: ) -
E1.3
A rectangular channel has a bottom width of and Manning’s
-
(a)
Determine the slope to give a normal depth of when the discharge is
-
(b)
Determine the critical slope and the critical depth when the discharge is
-
(c)
Determine the critical slope to give a the critical depth of and compute the corresponding discharge.
(Answer:(a) , (b) , , (c) , )
-
(a)
-
E1.4
For a trapezoidal channel with a base width , Manning’s and side slope (i.e. 1 vertical: 2 horizontal), calculate the critical depth, critical velocity, and critical slope if its discharge .
(Answer:, s, ) -
E1.5
A rectangular channel wide carries of water when flowing deep. Work out the flow’s specific energy. Is the flow sub-critical or super-critical?
(Answer: m and flow is sub-critical) -
E1.6
Two engineers observed two rivers and recorded the following flow parameters: River 1: flow discharge , flow velocity , water surface width ; River 2: flow discharge , flow velocity , water surface width . Decide the flow regime of two rivers, i.e. sub-critical or super-critical.
(Answer: River 1 is sub-critical and River 2 is super-critical) -
E1.7
A concrete, trapezoidal channel has a bottom slope of and a Manning roughness factor of . The bottom width of the channel is , and the side slopes are 1 in 2. Determine the velocity and discharge when the flow is normal at a depth of .
(Answer: , ) -
E1.8
A trapezoidal channel has a bottom slope of in and a Manning roughness factor of . The bottom width of the channel is , and the side slopes are 1 in 3. Determine the normal depth in this channel for .
(Answer: ). -
E1.9
The flow discharge in uniform flow in a rectangular channel wide is when the slope is 1:100. Is the flow sub-critical or super-critical? Calculate the slope, , that would give critical depth. The Manning roughness coefficient is .
(Answer: super-critical, , ).Compound Channels
-
E1.10
The cross-section of a stream can be approximated by the compound channel shown in figure 2. The bottom slope is . The Manning roughness factor for the main channel and for the overbank areas. Determine the normal depth for a discharge of . Also, calculate the energy coefficient and the momentum coefficient for the channel with this flow condition.
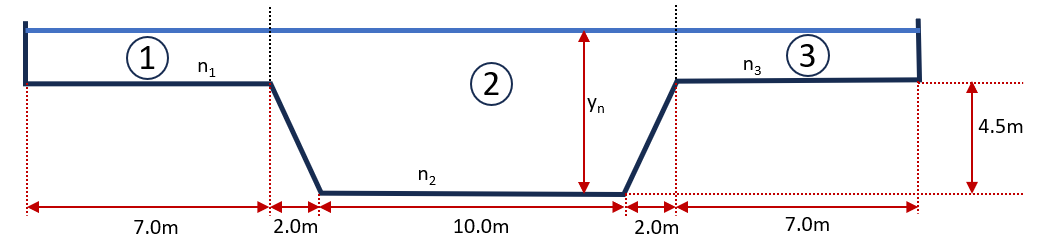
Figure 2: A Compound section (Answer: , , .)
-
E1.11
The total width of the channel considered in Question E1.10 is to be decreased by reducing the overbank portions symmetrically; however, this reduction must not cause an increase of more than in the flow depth for the discharge of . Assuming normal depth still is present in the channel, determine the minimum allowable channel total width, .
(Answer: .) -
E1.12
The cross-section of a river with flood plains flowing in uniform flow may be idealized as shown in Fig. 3. Determine the discharge carried by the river when its dimensions and roughness parameters are:
Bed slope:
Manning’s ns:
Side slopes:
Bed widths: , ,
Main channel depth:and
Normal depth
(Answer: .)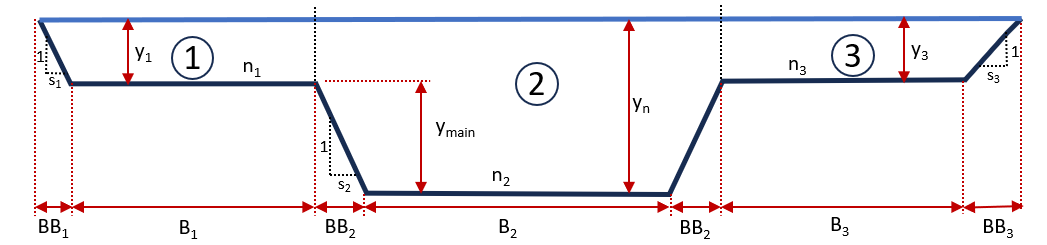
Figure 3: Idealized river channel with flood plains -
E1.13
For the channel of question E1.12 calculate the flow, if all dimensions, including the normal depth were the same, but the slope of the channel is 0.002.
(Answer ).Efficient Channels
-
E1.14
A trapezoidal channel has side slopes of 1:3/4 and the slope of the bed is 1 in 2000. Determine the optimum dimensions of the channel if it is to carry water at . Use the Chezy formula, assuming that .
(Answer: , ). -
E1.15
An open channel with is to be designed to carry of water at a slope of 0.0065. Find the most efficient cross-section for a rectangular section.
(Answer: ). -
E1.16
A rectangular channel has width and normal depth . What is the diameter of a semicircular channel that will have the same discharge as in the rectangular channel, when flowing just full in uniform flow? Assume that and are the same in the two cases. Compare the two wetted perimeters.
(Answer: , , ) -
E1.17
What are the dimensions of the most efficient rectangular channel section to carry at a slope of 1 in 900. The surface of the channel is of concrete.
(Answer: , using ) -
E1.18
What is the most efficient depth for a brick channel of a trapezoidal section with sides sloping at to the horizontal to carry . The bed slope is 0.0009.
(Answer: , using )